…and why it doesn’t work for a quantum alternating group
Despite problems around its existence being well-known, the Google search “quantum alternating group” only gets one (relevant) hit. This is to a paper of Freslon, Teyssier, and Wang, which states:
We therefore have to resort to another idea, which is to compare the process with the so-called pure quantum transposition random walk and prove that they asymptotically coincide. This is a specifically quantum phenomenon connected to the fact that the pure quantum transposition walk has no periodicity issue because there is no quantum alternating group.
Let us explain this a little. Take a deck of  cards, say in some known order. What we are going to do is take two (different) cards at random, and swap them. The question is, does this mix up the deck of cards? What does this question mean? Let
cards, say in some known order. What we are going to do is take two (different) cards at random, and swap them. The question is, does this mix up the deck of cards? What does this question mean? Let  be the order of the cards after
be the order of the cards after  of these pure random transposition shuffles. If the shuffles mix up the cards then:
of these pure random transposition shuffles. If the shuffles mix up the cards then:
![\displaystyle \lim_{k\to\infty}\mathbb{P}[\xi_k=\sigma]=\frac{1}{N!}\qquad(\sigma\in S_{N})](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Clim_%7Bk%5Cto%5Cinfty%7D%5Cmathbb%7BP%7D%5B%5Cxi_k%3D%5Csigma%5D%3D%5Cfrac%7B1%7D%7BN%21%7D%5Cqquad%28%5Csigma%5Cin+S_%7BN%7D%29&bg=ffffff&fg=545454&s=0&c=20201002) .
.
The random variable  is a product of
is a product of  transpositions and using the sign group homomorphism:
transpositions and using the sign group homomorphism:
 .
.
Take a permutation 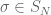 of odd sign, then:
of odd sign, then:
![\displaystyle \lim_{k\to\infty}\mathbb{P}[\xi_{2k}=\sigma]=0,](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Clim_%7Bk%5Cto%5Cinfty%7D%5Cmathbb%7BP%7D%5B%5Cxi_%7B2k%7D%3D%5Csigma%5D%3D0%2C&bg=ffffff&fg=545454&s=0&c=20201002)
and so this pure random transposition shuffle cannot mix up the deck of cards. The order of the deck alternates (geddit) between  , the alternating group, and
, the alternating group, and  , the complement of
, the complement of 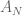 in
in  (if we allow the two cards to be chosen independently, so that there is a chance we pick the same card twice, and do a do-nothing shuffle, then this barrier disappears and this random transposition shuffle does mix up the cards. See Diaconis & Shahshahani).
(if we allow the two cards to be chosen independently, so that there is a chance we pick the same card twice, and do a do-nothing shuffle, then this barrier disappears and this random transposition shuffle does mix up the cards. See Diaconis & Shahshahani).
Amaury Freslon instigated a study of a quantum version of the above random walk. The probability distribution of the shuffles above is:
 .
.
The measure  is the measure uniform on transpositions in
is the measure uniform on transpositions in  . No such measure makes direct sense in the quantum setting, but if we recast this measure as the measure constant on permutations with
. No such measure makes direct sense in the quantum setting, but if we recast this measure as the measure constant on permutations with  fixed points there is a direct analogue,
fixed points there is a direct analogue,  (see Section 4 for details).
(see Section 4 for details).
If 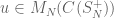 is the fundamental representation, and
is the fundamental representation, and ![u^c=[\mathbf{1}_{j\to i}]_{i,n=1,...,N}](https://s0.wp.com/latex.php?latex=u%5Ec%3D%5B%5Cmathbf%7B1%7D_%7Bj%5Cto+i%7D%5D_%7Bi%2Cn%3D1%2C...%2CN%7D&bg=ffffff&fg=545454&s=0&c=20201002) , an element of
, an element of  , the entry-wise abelianisation, the trace
, the entry-wise abelianisation, the trace  counts the number of fixed points. The functions
counts the number of fixed points. The functions  asking of a permutation, do you map
asking of a permutation, do you map  ? One for yes, zero for no:
? One for yes, zero for no:
 .
.
Freslon’s  can be thought of as the measure uniform on those quantum permutations that satisfy
can be thought of as the measure uniform on those quantum permutations that satisfy  .
.
If you shuffle according to classical  , you meet the periodicity issue associated with
, you meet the periodicity issue associated with  . However, there is no such periodicity issue in the quantum case, because there is nothing analogous to a quantum sign homomorphism:
. However, there is no such periodicity issue in the quantum case, because there is nothing analogous to a quantum sign homomorphism:
 .
.
The classical alternating group is:
 ,
,
but with no quantum sign, we don’t seem to be able to define a quantum alternating group in the same way.
This is related to difficulties around the determinant (equal to the sign for permutation matrices). I think, but would have to check, that we can quotient  by the relation
by the relation  , and you get
, and you get  in that case… but problems with the determinant mean this cannot happen in the quantum case.
in that case… but problems with the determinant mean this cannot happen in the quantum case.
Private communication has shown me a proof that if you quotient any compact matrix quantum group with  , then you get a commutative algebra, that is, a classical group. In particular,
, then you get a commutative algebra, that is, a classical group. In particular,
 ,
,
and not something non-commutative, corresponding to a quantum alternating group  .
.
Another way?
This no-go result, which is cool but unpublished, doesn’t rule out a quantum alternating group of the form:
 .
.
There is indeed for every  a genuine quantum group
a genuine quantum group  with
with  , but this quantum group does not sit nicely as a quantum subgroup of
, but this quantum group does not sit nicely as a quantum subgroup of  (from here, Section 4).
(from here, Section 4).
Given a quantum permutation group  , the set of characters on universal
, the set of characters on universal  forms a group
forms a group  , the classical version of
, the classical version of  . The group law is convolution:
. The group law is convolution:
 .
.
I have a particular interest in characters, and have a pre-print (Section 4) doing some analysis on them. Let  be a character. Then, applying what I call the Birkhoff slice (Section 4.1),
be a character. Then, applying what I call the Birkhoff slice (Section 4.1),  , applying a state to the fundamental magic representation component-wise, gives a permutation matrix:
, applying a state to the fundamental magic representation component-wise, gives a permutation matrix:
 .
.
In this case we write  , and where
, and where  is the abelianisation,
is the abelianisation,  :
:
 .
.
The characters have support projections, and these in general do not live in  but in the bidual
but in the bidual  . These support projections live in the strong closure of
. These support projections live in the strong closure of  in its bidual. Briefly, let:
in its bidual. Briefly, let:
 .
.
(as an aside, if we transpose in  the indices, so
the indices, so  instead of
instead of  , then
, then  .)
.)
It turns out that the support projection  of
of  is the strong limit of
is the strong limit of  … and if
… and if  converges to zero… then
converges to zero… then  is zero, not a character, and
is zero, not a character, and  is not in the classical version of
is not in the classical version of  .
.
Enter this talk by Gilles Gonçalves De Castro (Universidade Federal de Santa Catarina, Brazil), who teaches us with his coauthor Giulioano Boava that it is possible to include (admissible) strong as well as norm relations in defining a universal  -algebra.
-algebra.
An idea!
So, why not take  , or rather
, or rather  , and quotient out the characters in the complement of
, and quotient out the characters in the complement of 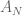 in
in  ? We can do this via the relations
? We can do this via the relations  for
for  , they are admissible. So… define the following algebra:
, they are admissible. So… define the following algebra:

There is a lot of work to do here to prove that this is a quantum group… have we a *-homomorphism  ? But at least we have a candidate algebra.
? But at least we have a candidate algebra.
Failure
Actually we don’t. In fact, either the algebra does not admit a quantum group structure OR
 ,
,
Unfortunately, because of non-coamenability issues, lots of algebras of continuous functions on quantum permutation groups also have  for all
for all  … not because they have no classical versions, but because classical versions are defined on the universal level… where there are always characters… at the reduced level the algebras admit no characters.
… not because they have no classical versions, but because classical versions are defined on the universal level… where there are always characters… at the reduced level the algebras admit no characters.
In particular, the reduced algebra of functions  satisfies
satisfies  for all
for all 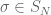 , and so, if we assume that
, and so, if we assume that  DOES have a quantum group structure, we have a comultiplication preserving quotient:
DOES have a quantum group structure, we have a comultiplication preserving quotient:
 .
.
Then with the help of J. De Ro, this means we have a Hopf*-algebra morphism on the level of the dense Hopf*-algebras, saying that  is a quantum subgroup of
is a quantum subgroup of  . But of course this
. But of course this  is a quantum subgroup of
is a quantum subgroup of  and so it follows in this case that the two quantum groups coincide.
and so it follows in this case that the two quantum groups coincide.
This isn’t a great no-go theorem: but a log of something that doesn’t work. And of course this approach doesn’t work for any subgroup of  .
.


Recent Comments