Category Archive

You are currently browsing the category archive for the ‘General’ category.

The relationship between password strength, length, and alphabet

March 31, 2024 in General | Leave a comment

This is just a little exercise in partial differentiation

Introduction

So, you have a password of length L from an alphabet A. Suppose you have a choice to increase the length, L\to L+1, vs the alphabet size |A|\to |A|+1. Which will make your password more secure?

In this sense we will assume that passwords are subject only to random guesses, and so we make the simple assumption that given the data (|A|,L), the larger the number of possible passwords, the more secure the password.

The set of passwords is \underbrace{A\times A\times \cdots \times A}_{L\text{ times}}. This has size |A|^L.

Simple Numerics

A simple approach is to simply make a table:

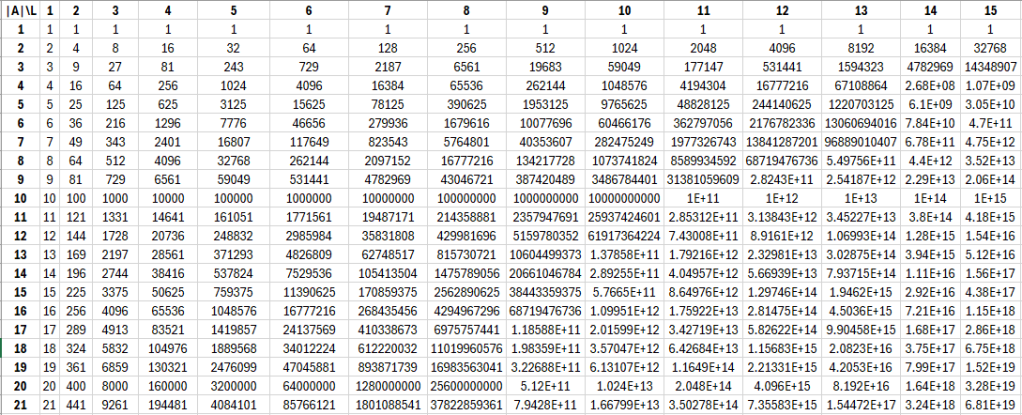
An eyeballing of this will tell you that most of time it appears that increasing the length is preferable to increasing the alphabet size. But then again, alphabet size jumps tend to be larger, e.g. 26 to 52, 52 to 62, etc.

Suppose you have a length L password from the alphabet A=\{a,b,\dots,z\}. Are you better off going to length L, or going to the alphabet of size 62, with the capital letters and the numebers? As it happens, it depends on L. For L<5, you should increase the length, but for L\geq 6, you should double the size of the alphabet. This is typical.

Some analysis

Consider a password from a set of |A|^L. Consider the two options, for constant \alpha,\beta:

  • increase the alphabet size: |A|\to \alpha|A|, or
  • increase the password length L\to L+\beta.

If we look what these do to the number of passwords:

  • |A|^L\to (\alpha|A|)^L\to \alpha^L|A|^L vs
  • |A|^{L+\beta}\to |A|^\beta|A|^L,

we are comparing \alpha^L to |A|^\beta, and \alpha,\,\beta are constant, we are comparing the exponential function x\mapsto \alpha^x and the polynomial function x\mapsto x^\beta. While increasing the password length initially can do better, as |A| and particularly L increases, the exponential function speeds past the polynomial function, so eventually, it will make more sense to increase the alphabet size. Our eyeballing has let us down.

For example, from the table above, at |A|=20 and L=14, it doesn’t appear to be even close, here at \alpha=21/20, and \beta=1, you get far more security increasing the length.

But for a fixed |A|=20, there exists a length for which it makes more sense to increase the alphabet by a factor of 21/20. The answer is 61.

So, if you have a length 61 password from an alphabet of size 20, you are better off increasing the alphabet size.

I guess what is relevant here are the following questions: at |A|=26,\,52,\,62,\,94 (adding the special characters), what are the answers?

  • If |A|=26, and L<5, you could increase the length of the password rather than jumping to |A|=52.
  • If |A|=52, and L<23, you could increase the length of the password rather than jumping to |A|=62.
  • If |A|=62, and L<10, you could increase the length of the password rather than jumping to |A|=94.

Going to special characters only makes sense in our framework if there is also a password length condition of 10 or more.

Partial Differentiation

This wasn’t even what I wanted to do here, which was to approximate this question using partial differentiation. In all these questions we are asking about what happens to |A|^L when we change |A| and keep L constant and vice versa. So partial differentiation. I guess the problem is |A| and L are discrete, rather than continuous, but sure x^L and |A|^x are perfectly good functions to differentiate. Let N:=|A|^L.

Even I can differentiate with respect to |A| (in fact, on first go I wrote with respect to L here, and got it wrong!):

\displaystyle \dfrac{\partial N}{\partial |A|}=L\cdot |A|^{L-1}.

We might use some logs to differentiate with respect to L:

\ln(N)=\ln(|A|^L)

\ln(N)=L\cdot \ln(|A|)

\displaystyle \implies \dfrac{1}{N}\dfrac{\partial N}{\partial L}=\ln(|A|)

\displaystyle \implies \dfrac{\partial N}{\partial |A|}=N\ln(|A|)=\ln |A|\cdot |A|^L.

These partial derivatives estimate that if |A|\to \alpha|A| (a change of (\alpha-1)|A| and L\to L+\beta,

\Delta N\approx \dfrac{\partial N}{\partial |A|}\Delta |A|=L|A|^{L-1}(\alpha-1)|A|=(\alpha-1)L|A|^L=(\alpha-1)LN

\Delta N\approx \dfrac{\partial N}{\partial L}\Delta L=\ln |A|\cdot |A|^L\beta=\beta \ln(|A|)N,

so, approximately, we are left comparing \beta \ln(|A|) and (\alpha-1)\cdot L. And here we see \ln(|A|) vs L… eventually L\gg \ln(|A|) if both grow, giving us the same answer as before.

Third Level Maths Grinds in Cork

March 5, 2024 in General, Grinds, Leaving Cert | Leave a comment

I am now available to help students at all levels in the Glanmire and Bishopstown areas.

Contact me on  086-1089437 or jpmccarthymaths@gmail.com.

A probability question on card shuffling

November 17, 2023 in General, Probability Theory | Leave a comment

Alice, Bob and Carol are hanging around, messing with playing cards.

Alice and Bob each have a new deck of cards, and Alice, Bob, and Carol all know what order the decks are in.

Carol has to go away for a few hours.

Alice starts shuffling the deck of cards with the following weird shuffle: she selects two (different) cards at random, and swaps them. She does this for hours, doing it hundreds and hundreds of times.

Bob does the same with his deck.

Carol comes back and asked “have you mixed up those decks yet?” A deck of cards is “mixed up” if each possible order is approximately equally likely:

\displaystyle \mathbb{P}[\text{ deck in order }\sigma\in S_{52}]\approx \frac{1}{52!}

She asks Alice how many times she shuffled the deck. Alice says she doesn’t know, but it was hundreds, nay thousands of times. Carol says, great, your deck is mixed up!

Bob pipes up and says “I don’t know how many times I shuffled either. But I am fairly sure it was over a thousand”. Carol was just about to say, great job mixing up the deck, when Bob interjects “I do know that I did an even number of shuffles though.“.

Why does this mean that Bob’s deck isn’t mixed up?

A connection between numerical solutions to the Laplace and Heat Equations

June 10, 2020 in General, MATH7016 | Leave a comment

I am not sure has the following observation been made:

When the Jacobi Method is used to approximate the solution of Laplace’s Equation, if the initial temperature distribution is given by T^0(\mathbf{x}), then the iterations T^{\ell}(\mathbf{x}) are also approximations to the solution, T(\mathbf{x},t), of the Heat Equation, assuming the initial temperature distribution is T^0(\mathbf{x}).

I first considered such a thought while looking at approximations to the solution of Laplace’s Equation on a thin plate. The way I implemented the approximations was I wrote the iterations onto an Excel worksheet, and also included conditional formatting to represent the areas of hotter and colder, and the following kind of output was produced:

Let me say before I go on that this was an implementation of the Gauss-Seidel Method rather than the Jacobi Method, and furthermore the stopping rule used was the rather crude |T^{\ell+1}_{i,j}-T^{\ell}_{i,j}|<\varepsilon.

However, do not the iterations resemble the flow of heat from the heat source on the bottom through the plate? The aim of this post is to investigate this further. All boundaries will be assumed uninsulated to ease analysis.

Discretisation

Consider a thin rod of length L. If we mesh the rod into n pieces of equal length \Delta x=L/n, we have discretised the rod, into segments of length \Delta x, together with ‘nodes’ 0=x_0<\Delta x=x_1<2\Delta x=x_2<\cdots<n\Delta x=L=x_n.

Suppose are interested in the temperature of the rod at a point x\in[0,L], T(x). We can instead consider a sampling of T, at the points x_i:

\displaystyle T(x_i)=T(i\Delta x)=:T_i.

Similarly we can mesh a plate of dimensions W\times H into an n\times m rectangular grid, with each rectangle of area \Delta x\Delta y, where n\Delta x=W and m\Delta y=H, together with nodes x_{i,j}=(i\Delta x,j\Delta y), and we can study the temperature of the plate at a point \mathbf{x}\in[0,W]\times [0,H] by sampling at the points x_{i,j}:

\displaystyle T(x_{i,j})=T(i\Delta x,j\Delta y)=:T_{i,j}.

We can also mesh a box of dimension W\times D\times H into an n_1\times n_2\times n_2 3D grid, with each rectangular box of volume \Delta x\Delta y\Delta z, where n_1\Delta x=W, n_2\Delta y=D, and n_3\Delta z=H, together with nodes x_{i,j,k}=(i\Delta x,j\Delta y,k\Delta z), and we can study the temperature of the box at the point \mathbf{x}\in [0,W]\times [0,D]\times [0,H] by sampling at the points x_{i,j,k}:

\displaystyle T(x_{i,j,k})=T(i\Delta x,j\Delta y,k\Delta z)=:T_{i,j,k}.

Finite Differences

How the temperature evolves is given by partial differential equations, expressing relationships between T and its rates of change.

Read the rest of this entry »

An A to Z of Mathematics vs Physics

June 10, 2020 in General | Leave a comment

We are the mathematicians and they are the physicists (all jibes and swipes are to be taken lightly!!)

A

A is for atom and axiom. While we build beautiful universes from our carefully considered axioms, they try and destroy this one by smashing atoms together.

B

B is for the Banach-Tarski Paradox, proof if it was ever needed that the imaginary worlds which we construct are far more interesting then the dullard of a one that they study.

C

C is for Calculus and Cauchy. They gave us calculus about 340 years ago: it only took us about 140 years to make sure it wasn’t all nonsense! Thanks Cauchy!

D

D is for Dimension. First they said there were three, then Einstein said four, and now it ranges from 6 to 11 to 24 depending on the day of the week. No such problems for us: we just use n.

E

E is for Error Terms. We control them, optimise them, upper bound them… they just pretend they’re equal to zero.

F

F is for Fundamental Theorems… they don’t have any.

G

G is for Gravity and Geometry. Ye were great yeah when that apple fell on Newton’s head however it was us asking stupid questions about parallel lines that allowed Einstein to formulate his epic theory of General Relativity.

H

H is for Hole as in the Black Hole they are going to create at CERN.

I

I is for Infinity. In the hand of us a beautiful concept — in the hands of you an ugliness to be swept under the carpet via the euphemism of “renormalisation”…

J

J is for Jerk: the third derivative of displacement. Did you know that the fourth, fifth, and sixth derivatives are known as Snap, Crackle, and Pop? No, I did not know they had a sense of humour either.

K

K is for Knot Theory. A mathematician meets an experimental physicist in a bar and they start talking.

  • Physicist: “What kind of math do you do?”,
  • Mathematician: “Knot theory.”
  • Physicist: “Yeah, Me neither!”

L

L is for Lasers. I genuinely spent half an hour online looking for a joke, or a pun, or something humorous about lasers… Lost Ample Seconds: Exhausting, Regrettable Search.

M

M is for Mathematical Physics: a halfway house for those who lack the imagination for mathematics and the recklessness for physics.

N

N is for the Nobel Prize, of which many mathematicians have won, but never in mathematics of course. Only one physicist has won the Fields Medal.

O

O is for Optics. Optics are great: can’t knock em… 7 years bad luck.

P

P is for Power Series. There are rules about wielding power series; rules that, if broken, give gibberish such as the sum of the natural numbers being -\frac{1}{12}. They don’t care: they just keep on trucking.

Q

Q is for Quark… they named them after a line in Joyce as the theory makes about as much sense as Joyce.

R

R is for Relativity. They are relatively pleasant.

S

S is for Singularities… instead of saying “we’re stuck” they say “singularity”.

T

T is for Tarksi… Tarski had a son called Jon who was a physicist. Tarksi always appears twice.

U

U is for the Uncertainty Principle. I am uncertain as to whether writing this was a good idea.

V

V is for Vacuum… Did you hear about the physicist who wanted to sell his vacuum cleaner? Yeah… it was just gathering dust.

W

W is for the Many-Worlds-Interpretation of Quantum Physics, according to which, Mayo GAA lose All-Ireland Finals in infinitely many different ways.

X

X is unknown.

Y

Y is for Yucky. Definition: messy or disgusting. Example: Their “Calculations”

Z

Z is for Particle Zoo… their theories are getting out of control. They started with atoms and indeed atoms are only the start. Pandora’s Box has nothing on these people.. forget baryons, bosons, mesons, and quarks: the latest theories ask for sneutrinos and squarks; photinos and gluinos, zynos and even winos. A zoo indeed.

PS

We didn’t even mention String Theory!

The End.

A Uniqueness Problem

May 1, 2020 in General | Leave a comment

A colleague writes (extract):

“I have an assessment with 4 sections in it A,B,C and D.

I have a question bank for each section. The number of questions in each bank is A-10, B-10, C-5, D-5.

In my assessment I will print out randomly a fixed number of questions from each bank. Section A will have 5 questions, B-5, C-2, D-2. 14 questions in total appear on the exam.

I can figure out how many different exam papers (order doesn’t matter) can be generated (I think!).

\displaystyle \binom{10}{5}\cdot \binom{10}{5}\cdot \binom{5}{2}\cdot \binom{5}{2}=6350400

But my question is: what is the uniqueness of each exam, or what overlap between exams can be expected.?

I am not trying to get unique exams for everyone (unique as in no identical questions) but would kinda like to know what is the overlap.“

Following the same argument as here we can establish that:

Fact 1

The expected number of students to share an exam is \approx 0.00006.

Let the number of exams \alpha:=6350400.

This is an approach that takes advantage of the fact that expectation is linear, and the probability of an event E not happening is

\displaystyle\mathbb{P}[\text{not-}E]=1-\mathbb{P}[E].

Label the 20 students by i=1,\dots,20 and define a random variable S_i by

\displaystyle S_i=\left\{\begin{array}{cc}1&\text{ if student i has the same exam as someone elese} \\ 0 & \text{ if student i has a unique exam}\end{array}\right.

Then X, the number of students who share an exam, is given by:

\displaystyle X=S_1+S_2+\cdots+S_{20},

and we can calculate, using the linearity of expectation.

\mathbb{E}[X]=\mathbb{E}[S_1]+\cdots \mathbb{E}[S_{20}].

The S_i are not independent but the linearity of expectation holds even when the addend random variables are not independent… and each of the S_i has the same expectation. Let p be the probability that student i does not share an exam with anyone else; then

\displaystyle\mathbb{E}[S_i]=0\times\mathbb{P}[S_i=0]+1\times \mathbb{P}[S_i=1],

but \displaystyle\mathbb{P}[S_i=0]=\mathbb{P}[\text{ student i does not share an exam}]=p, and

\displaystyle \mathbb{P}[S_i=1]=\mathbb{P}[\text{not-}(S_i=0)]=1-\mathbb{P}[S_i=0]=1-p,

and so

\displaystyle\mathbb{E}[S_i]=1-p.

All of the 20 S_i have this same expectation and so

\displaystyle\mathbb{E}[X]=20\cdot (1-p).

Now, what is the probability that nobody shares student i‘s exam?

We need students 1\rightarrow i-1 and i+1\rightarrow 20 — 19 students — to have different exams to student i, and for each there is \alpha-1 ways of this happening, and we do have independence here (student 1 not sharing student i‘s exam doesn’t change the probability of student 2 not sharing student i‘s exam), and so \mathbb{P}[\text{(student j not sharing) AND (student k not sharing)}] is the product of the probabilities.

So we have that

\displaystyle p=\left(\frac{\alpha-1}{\alpha}\right)^{19},

and so the answer to the question is:

\displaystyle\mathbb{E}[X]=20\cdot \left(1-\left(\frac{\alpha-1}{\alpha}\right)^{19}\right)\approx 0.00005985\approx 0.00006.

We can get an estimate for the probability that two or more students share an exam using Markov’s Inequality:

\displaystyle\mathbb{P}[X\geq 2]\leq \frac{\mathbb{E}[X]}{2}\approx 0.00003=0.003\%

Fact 2

This estimate is tight: the probability that two or more students (out of 20) share an exam is about 0.003%.

This tallies very well with the exact probability which can be found using a standard Birthday Problem argument (see the solution to Q. 7 here) to be:

\mathbb{P}[X\geq 2]\approx 0.0000299191\approx 0.003\%

The probability that two given students share an exam is 1/\alpha\approx 0.00001575\%

Fact 3

The expected number of shared questions between two students is 6.6

Take students 1 and 2. The questions are in four bins: two of ten, two of five. Let B_i be the number of questions in bin i that students 1 and 2 share. The expected number of shared questions, Q, is:

\displaystyle \mathbb{E}[Q]=\sum_{i=1}^4\mathbb{E}[B_i],

and the numbers are small enough to calculate the probabilities exactly using the hypergeometric distribution.

The calculations for bins 1 and 2, and bins 3 and 4 are the same. The expectation

\displaystyle\mathbb{E}[B_1]=\sum_{j=0}^5j\mathbb{P}[B_1=j].

Writing briefly p_j=\mathbb{P}[B_1=j], looking at the referenced hypergeometric distribution we find:

\displaystyle p_j=\frac{\binom{5}{j}\binom{5}{5-j}}{\binom{10}{5}}

and we find:

\displaystyle\mathbb{E}[B_1]=\mathbb{E}[B_2]=\frac52

Similarly we see that

\displaystyle\mathbb{E}[B_3]=\mathbb{E}[B_4]=\frac{4}{5}

and so, using linearity:

\displaystyle\mathbb{E}[Q]=\frac52+\frac52+\frac45+\frac45=6.6

This suggests that on average students share about 50% of the question paper. Markov’s Inequality gives:

\displaystyle\mathbb{P}[Q\geq 7]\underset{\approx}{\leq} 0.9429,

but I do not believe this is tight.

Calculating this probability exactly is tricky because there are many different ways that students can share a certain number of questions. We would be looking at something like “multiple hypergeometric”, and I would calculate it as the event not-(0 or 1 or 2 or 3 or 4 or 5 or 6).

I think the \mathbb{E}[Q]=6.6 result is striking enough at this time!

Four Flavours of De Morgan

January 31, 2020 in General, MATH6038, MATH6055 | Leave a comment

We tell four tales of De Morgan.

In each case we have something that looks like AND, something that looks like OR, and something that looks like NOT.

Sets

The Collection of Objects

Consider a universe of discourse/universal set/ambient set  U. When talking about people this might be the collection of all people. When talking about natural numbers this might be the set \mathbb{N}. When talking about real numbers this might be the set \mathbb{R}. When talking about curves it might be the set of subsets of the plane, \mathcal{P}(\mathbb{R}\times \mathbb{R}), etc.

The collection of objects in this case is the set of subsets of U, denoted \mathcal{P}(U).

Suppose, for the purposes of illustration, that

U=\{1,2,3,4,5\}.

Consider the subsets A=\{2,3,5\}, and B=\{1,3,5\} .

in the obvious way.

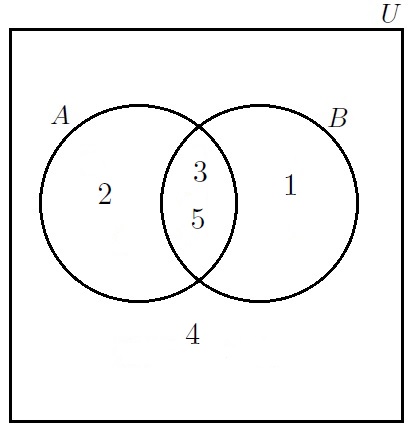
AND

Note that two objects are contained both in A AND in B. We call the set of such objects the intersection of A AND B, A\cap B:

A\cap B=\{3,5\}.

We can represent the ambient set U, as well as the sets A and B — and the fact that they intersect — using a Venn Diagram:

graph1

We can demonstrate for a general A and B ‘where’ the intersection is:

Venn2.jpg

Read the rest of this entry »

Pure Mathematics: What’s the Point?

December 19, 2019 in General | Leave a comment

Slides of a talk given at CIT School of Science Seminar.

Contexts & Concepts

January 11, 2019 in General, MATH7019, MATH7021 | Leave a comment

Talk delivered to the Conversations on Teaching and Learning Winter Programme 2018/19, organised by the Teaching & Learning Unit in CIT (click link for slides):

Contexts and Concepts: A Case Study of Mathematics Assessment for Civil & Environmental Engineering

Expected Number of Shared Birthdays

November 28, 2018 in General | 1 comment

I received the following email (extract) from a colleague:

With the birthday question the chances of 23 people having unique birthdays is less than ½ so probability of shared birthdays is greater than 1-in-2. 

Coincidentally on the day you sent out the paper, the following question/math fact was in my son’s 5th Class homework.

We are still debating the answer, hopefully you could clarify…

In a group of 368 people, how many should share the same birthday. There are 16×23 in 368 so there are 16 ways that 2 people should share same birthday (?) but my son pointed out, what about 3 people or 4 people etc.

I don’t think this is an easy problem at all.

First off we assume nobody is born on a leap day and the distribution of birthdays is uniform among the 365 possible birthdays. We also assume the birthdays are independent (so no twins and such).

They were probably going for 16 or 32 but that is wrong both for the reasons given by your son but also for the fact that people in different sets of 23 can also share birthdays.

The brute force way of calculating it is to call by X the random variable that is the number of people who share a birthday and then the question is more or less looking for the expected value of X, which is given by:

\displaystyle \mathbb{E}[X]=\sum_{i=2}^{368}i\cdot \mathbb{P}[X=i].

Already we have that \mathbb{P}[X=2]=\mathbb{P}[X=3]=0 (why), and \mathbb{P}[X=4] is (why) the probability that four people share one birthday and 364 have different birthdays. This probability isn’t too difficult to calculate (its about 10^{-165}) but then things get a lot harder.

For X=5, there are two possibilities:

  • 5 share a birthday, 363 different birthdays, OR
  • 2 share a birthday, 3 share a different birthday, and the remaining 363 have different birthdays

Then X=6 is already getting very complex:

  • 6 share a birthday, 362 different birthdays, OR
  • 3, 3, 362
  • 4, 2, 362
  • 2, 2, 2, 362

This problem is spiraling out of control.

 

There is another approach that takes advantage of the fact that expectation is linear, and the probability of an event E not happening is

\displaystyle\mathbb{P}[\text{not-}E]=1-\mathbb{P}[E].

Label the 368 people by i=1,\dots,368 and define a random variable S_i by

\displaystyle S_i=\left\{\begin{array}{cc}1&\text{ if person i shares a birthday with someone else} \\ 0 & \text{ if person i does not share a birthday}\end{array}\right.

Then X, the number of people who share a birthday, is given by:

\displaystyle X=S_1+S_2+\cdots+S_{368},

and we can calculate, using the linearity of expectation.

\mathbb{E}[X]=\mathbb{E}[S_1]+\cdots \mathbb{E}[S_{368}].

The S_i are not independent but the linearity of expectation holds even when the addend random variables are not independent… and each of the S_i has the same expectation. Let p be the probability that person i does not share a birthday with anyone else; then

\displaystyle\mathbb{E}[S_i]=0\times\mathbb{P}[S_i=0]+1\times \mathbb{P}[S_i=1],

but \displaystyle\mathbb{P}[S_i=0]=\mathbb{P}[\text{ person i does not share a birthday}]=p, and

\displaystyle \mathbb{P}[S_i=1]=\mathbb{P}[\text{not-}(S_i=0)]=1-\mathbb{P}[S_i=0]=1-p,

and so

\displaystyle\mathbb{E}[S_i]=1-p.

All of the 368 S_i have this same expectation and so

\displaystyle\mathbb{E}[X]=368\cdot (1-p).

Now, what is the probability that nobody shares person i‘s birthday?

We need persons 1\rightarrow i-1 and i+1\rightarrow 368 — 367 persons — to have different birthdays to person i, and for each there is 364/365 ways of this happening, and we do have independence here (person 1 not sharing person i‘s birthday doesn’t change the probability of person 2 not sharing person i‘s birthday), and so \mathbb{P}[\text{(person k not sharing) AND (person k not sharing)}] is the product of the probabilities.

So we have that

\displaystyle p=\left(\frac{364}{365}\right)^{367},

and so the answer to the question is:

\displaystyle\mathbb{E}[X]=368\cdot \left(1-\left(\frac{364}{365}\right)^{367}\right)\approx 233.54\approx 234.

There is possibly another way of answering this using the fact that with 368 people there are

\displaystyle \binom{368}{2}=67528

pairs of people.