Category Archive

You are currently browsing the category archive for the ‘Leaving Cert’ category.

Boxroom Mathematics: Episode I

May 2, 2020 in A1 Leaving Cert Maths, Boxroom Mathematics, Grinds, Leaving Cert | Leave a comment

The videos, here, comprise me going through a full Leaving Cert Higher Level Mathematics Paper, namely 2019, Paper 1.

They’re neither slick, perfect, nor as good as I would like them to be.

The videos are labelled in the descriptions, so if you are looking for, say, Q. 5 you can flick through the videos until you find the question you are looking for (e.g. Q. 5 starts at 17.05 here).

All students are looking for help: but perhaps the student that these videos are best placed to help is a student (eventually) going for a H1 who needs something to be explained in more depth, or to give the thought process behind attacking a more challenging problem.

Difficult Connected Particles Question

February 27, 2019 in Grinds, Leaving Cert Applied Maths | Leave a comment

When I say difficult, I mean difficult in comparison to the usual standard of Higher Level Leaving Cert Applied Maths Connected Particles Questions

Question (a)

Consider the following:

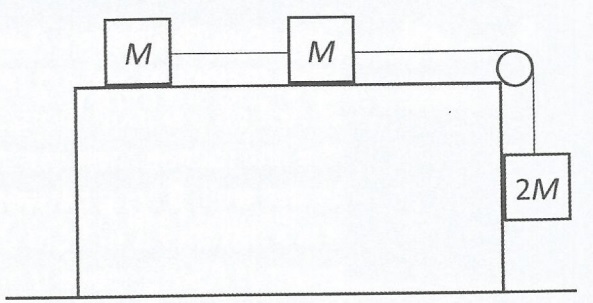
part1

A rectangular block moves across a stationary horizontal surface with acceleration $g/5$ (the question had $g/5$ m/s ${}^2$ but the m/s ${}^2$ is repeated as $g=9.8$ m/s ${}^2$ and so includes the unit).

There is a serious problem with this question and that is that the asymmetry in the problem means that there is an ambiguity: is the block moving left to right or right to left? I am going to assume the block moves from left to right. One would hope not to see such ambiguity in an official exam paper.

Two particles of mass $M$ placed on the block, are connected by a taut inextensible string. A second string passes over a light, smooth, fixed pulley to a third particle of mass $2M$ which presses against the block as shown in the diagram.

(i)

If contact between the particles and the block is smooth, find the magnitude and direction of the resultant forces acting on the particles.

Solution

Note firstly that there are two accelerations at play. The acceleration of the block relative to the horizontal surface, $g/5$ , and the accelerations of the particles relative to the block, say $a$ :

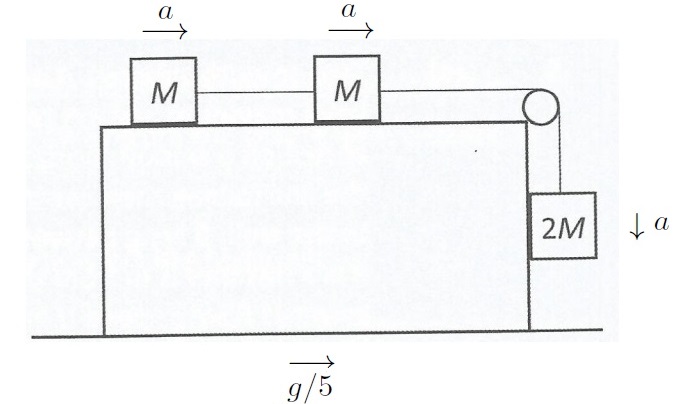
part2

We draw all the forces (I lazily didn’t add arrows to the force vectors):

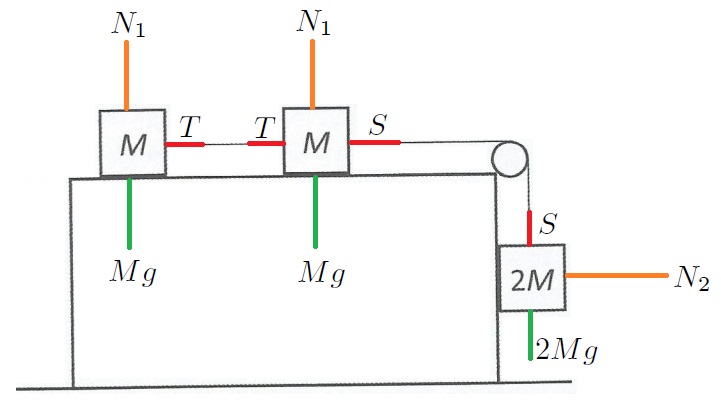
part3

We know that the normal forces for the particles on top of the block because their vertical acceleration is zero and so the sum of the forces in that direction must be zero, and as the down forces are equal for both, necessarily the up forces must be equal too.

Read the rest of this entry »

Another Relative Velocity Question

December 12, 2018 in Leaving Cert Applied Maths | Leave a comment

On a particular day the velocity of the wind, in terms of $\mathbf{i}$ and $\mathbf{j}$ , is $x\mathbf{i}-3\mathbf{j}$ , where $x\in\mathbb{N}$ .

$\mathbf{i}$ and $\mathbf{j}$ are unit vectors in the directions East and North respectively.

To a man travelling due East the wind appears to come from a direction North $\alpha^\circ$ West where $\tan\alpha=2$ .

When he travels due North at the same speed as before, the wind appears to come from a direction North $\beta^\circ$ West where $\tan\beta=3/2$ .

Find the actual direction of the wind.

Solution:

We start by writing

$\overrightarrow{V_{WM}}=\overrightarrow{V_W}-\overrightarrow{V_M}$ .

We have two equations.

Firstly, when the man travels due East, $\overrightarrow{V_M}=a\mathbf{i}$ for some constant $a$ . We have $\overrightarrow{V_W}=x\mathbf{i}-3\mathbf{j}$ and so

$\overrightarrow{V_{WM}}=(x-a)\mathbf{i}-3\mathbf{j}$ .

We know that this, with respect to the man, is coming from North $\alpha^\circ$ West. This means we have:

And furthermore:

$\displaystyle \tan\alpha=\frac{x-a}{3}\overset{!}{=}2$

$\Rightarrow x-a=6\Rightarrow a=x-6$ .

Now consider when the man travels due North, $\overrightarrow{V_M}=a\mathbf{j}$ . We have $\overrightarrow{V_W}=x\mathbf{i}-3\mathbf{j}$ still and so

$\overrightarrow{V_{WM}}=x\mathbf{i}-(3+a)\mathbf{j}$ .

We know that this, with respect to the man, is coming from North $\beta^\circ$ West. This means we have:

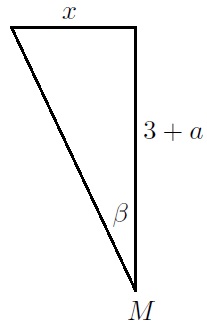
And furthermore:

$\displaystyle \tan\beta=\frac{x}{3+a}\overset{!}{=}\frac32$

$\underset{\times_{2(3+a)}}{\Rightarrow} 2x=9+3a$ ,

but we have $a=x-6$ and so

$2x=9+3(x-6)\Rightarrow x=9$ ,

so that $\overrightarrow{V_W}=9\mathbf{i}-3\mathbf{j}$ .

This means that the velocity of the wind looks like:

That is the wind comes from North $\theta$ West. We have that $\tan\theta=9/3\underset{\tan^{-1}}{\Rightarrow} \theta=\tan^{-1}(3)\approx 71.57^\circ$ , so the answer to the question asked is N $71.57^\circ$ W.

Relative Velocity Question Three Ways

December 12, 2018 in Leaving Cert Applied Maths | Leave a comment

Here we present three solutions to the one problem. The vector solution is probably the slickest. The geometry solution here can be simplified by being less rigorous, and the coordinate geometry solution might be made easier by using the $-b\pm\sqrt{\cdots}$ formula.

LCHL 2007, Q. 2(a)

Ship B is travelling west at 24 km/h. Ship A is travelling north at 32 km/h.
At a certain instant ship B is 8 km north-east of ship A.

(i) Find the velocity of ship A relative to ship B.

(ii) Calculate the length of time, to the nearest minute, for which the ships
are less than or equal to 8 km apart.

Solution to (i): We have that $\overrightarrow{V_A}=32\mathbf{j}$ and $\overrightarrow{V_B}=-24\mathbf{i}$ and so

$\overrightarrow{V_{AB}}=\overrightarrow{V_A}-\overrightarrow{V_B}=32\mathbf{j} -(-24\mathbf{i})=24\mathbf{i}+32\mathbf{j}$ .

Vector Approach to (ii)

First of all we draw a picture. As we are talking relative to ship B we will put B at the origin. If ship B is 8 km north-east of ship A then ship A is 8 km south-west of ship B.

rel1

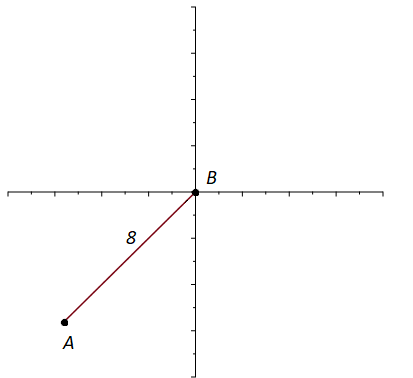
Where $\overrightarrow{R_0}$ is the initial displacement of ship A relative to ship B, the displacement of ship A relative to ship B, as a function of time, is given by

$\overrightarrow{R_{AB}}(t)=\overrightarrow{R_0}+t\cdot \overrightarrow{V_{AB}}$ .

Using some trigonometry — vertical and horizontal components of $\overrightarrow{R_0}$ — we have

$\displaystyle\overrightarrow{R_0}=-\frac{8}{\sqrt{2}}\mathbf{i}-\frac{8}{\sqrt{2}}\mathbf{j}$ ,

and so

$\displaystyle \overrightarrow{R_{AB}(t)}=\left(24t-\frac{8}{\sqrt{2}}\right)\mathbf{i}+\left(32t-\frac{8}{\sqrt{2}}\right)\mathbf{j}$ .

Read the rest of this entry »

On Parallel and Perpendicular Lines

June 5, 2018 in A1 Leaving Cert Maths, General, Grinds, Leaving Cert | Leave a comment

The purpose of this post is to briefly discuss parallelism and perpendicularity of lines in both a geometric and algebraic setting.

Lines

What is a line? In Euclidean Geometry we usually don’t define a line and instead call it a primitive object (the properties of lines are then determined by the axioms which refer to them). If instead points and line segments – defined by pairs of points $P,Q$ – $[PQ]$ are taken as the primitive objects, the following might define lines:

Geometric Definition Candidate

A line, $\ell$ , is a set of points with the property that for each pair of points in the line, $P,Q\in \ell$ ,

$[PQ]\cap \ell=[PQ]$ .

In terms of a picture this just says that when you have a line, that if you take two points in the line (the language in comes from set theory), that the line segment is a subset of the line:

line

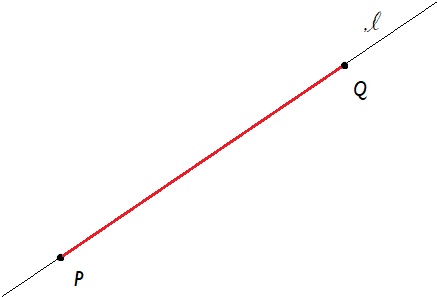
Exercise:

Why is this objectively not a good definition of a line.

Once we move into Cartesian\Coordinate Geometry we can perhaps do a similar trick. We can use line segments, and their lengths to define slope, (slope = rise over run) and then define a line as follows:

Algebraic Definition Candidate

A line, $\ell$ , is a set of points such that for all pairs of distinct points $P,Q\in\ell$ , the slope is a constant.

This means that if you take two pairs of distinct points in a line $\ell$ , and then calculate the slopes between them, you get the same answer, and therefore it makes sense to talk about the slope of a line, $m$ .

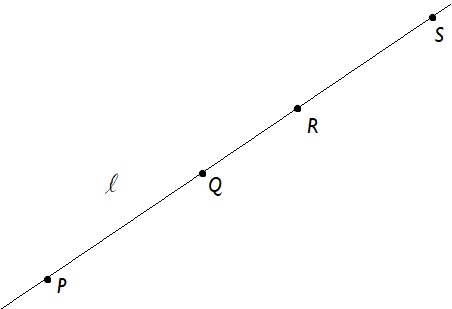
line2

This definition, however, has exactly the same problem as the previous. The definition we use isn’t too important but I do want to use a definition that considers the line a set of points.

The Equation of a Line

We can use such a definition to derive the equation of a line ‘formula’ for a line of slope $m$ containing a point $(x_1,y_1)$ .

Suppose first of all that we have an $x\text{-}y$ axis and a point $P(x_1,y_1)$ in the line. What does it take for a second point $Q(x,y)$ to be in the line?

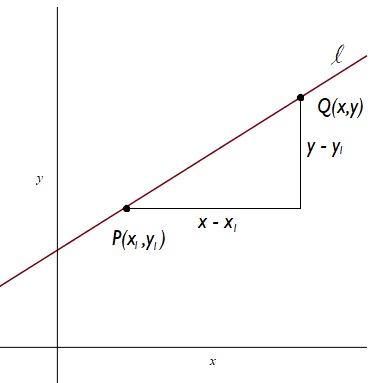
line4

Read the rest of this entry »

Some Leaving Cert Applied Maths Notes

April 23, 2018 in Leaving Cert Applied Maths | Leave a comment

For those planning on focusing on questions one to five and ten:

Applied Maths some Notes

The Line of Best Fit

March 2, 2018 in A1 Leaving Cert Maths, Data Science, General, Leaving Cert, MATH6000, MATH7019 | Leave a comment

“Straight-Line-Graph-Through-The-Origin”

The words of Mr Michael Twomey, physics teacher, in Coláiste an Spioraid Naoimh, I can still hear them.

There were two main reasons to produce this straight-line-graph-through-the-origin:

to measure some quantity (e.g. acceleration due to gravity, speed of sound, etc.)
to demonstrate some law of nature (e.g. Newton’s Second Law, Ohm’s Law, etc.)

We were correct to draw this straight-line-graph-through-the origin for measurement, but not always, perhaps, in my opinion, for the demonstration of laws of nature.

The purpose of this piece is to explore this in detail.

Direct Proportion

Two variables $P$ and $Q$ are in direct proportion when there is some (real number) constant $k$ such that $P=k\cdot Q$ .

Read the rest of this entry »

Writing a Cosine Plus Sine as a Sine

January 29, 2018 in A1 Leaving Cert Maths, General, Grinds, Leaving Cert, Leaving Cert Applied Maths, MATH6014 | Leave a comment

Occasionally, it might be useful to do as the title here suggests.

Two examples that spring to mind include:

solving $a\cdot\cos\theta\pm b\cdot\sin\theta=c$ for $\theta$ (relative velocity example with $-$ below)
maximising $a\cdot\cos\theta\pm b\cdot\sin\theta$ without the use of calculus

$a\cdot \cos\theta- b\cdot\sin\theta$

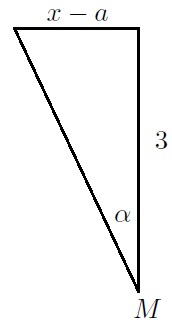
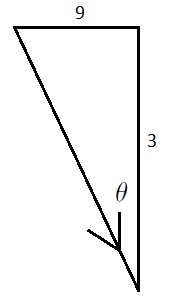
Note first of all the similarity between:

$\displaystyle a\cdot \cos\theta-b\cdot \sin \theta\sim \sin\phi\cos\theta-\cos\phi\sin\theta$ .

This identity is in the Department of Education formula booklet.

The only problem is that $a$ and $b$ are not necessarily sines and cosines respectively. Consider them, however, as opposites and adjacents to an angle in a right-angled-triangle as shown:

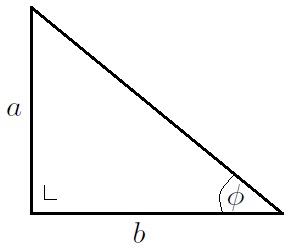
triangle

Using Pythagoras Theorem, the hypotenuse is $\sqrt{a^2+b^2}$ and so if we multiply our expression by $\displaystyle \frac{\sqrt{a^2+b^2}}{\sqrt{a^2+b^2}}$ then we have something:

$\displaystyle \frac{\sqrt{a^2+b^2}}{\sqrt{a^2+b^2}}\cdot \left(a\cdot \cos\theta- b\cdot\sin\theta\right)$

$\displaystyle=\sqrt{a^2+b^2}\cdot \left(\frac{a}{\sqrt{a^2+b^2}}\cos\theta-\frac{b}{\sqrt{a^2+b^2}}\sin\theta\right)$

$=\sqrt{a^2+b^2}\cdot \left(\sin\phi\cos\theta-\cos\phi\sin\theta\right)=\sqrt{a^2+b^2}\sin(\phi-\theta)$ .

Similarly, we have

$a\cdot\cos\theta+b\cdot \sin\theta=\sqrt{a^2+b^2}\sin(\phi+\theta)$ ,

where $\displaystyle\sin\phi=\frac{a}{\sqrt{a^2+b^2}}$ .

Read the rest of this entry »

The Principle of Conservation of Momentum for Pulleys

January 17, 2018 in Grinds, Leaving Cert Applied Maths | Leave a comment

Consider the following problem:

Two masses of 5 kg and 1 kg hang from a smooth pulley at the ends of a light inextensible string. The system is released from rest. After 2 seconds, the 5 kg mass hits a horizontal table:

i. How much further will the 1 kg mass rise?

ii. The 1 kg mass then falls and the 5 kg mass is jolted off the table. With what speed will the 5 kg mass begin to rise?

[6D Q. 4. Fundamental Applied Maths, 2nd Edition, Oliver Murphy]

It isn’t difficult to answer part i.: the answer is $\displaystyle \frac89 g$ m.

However how to treat part ii.? First of all a picture to help us understand this problem:

pulley

The 1 kg mass has dropped under gravity through a distance of $\displaystyle \frac89 g$ m. We can find the speed of the 1 kg mass using $u=0,a=g,s=\frac89 g$ . Alternatively, we can use Conservation of (Mechanical) Energy.

Taking the final position as $h=0$ , at its maximum height, the 1 kg mass has potential energy and no kinetic energy:

$\text{PE}_0=mgh=1g\frac89 g=\frac{8}{9}g^2$ .

When it reaches the point where the string is once again taut, it has not potential energy but the potential energy it had has been transferred into kinetic energy:

$\text{KE}_1=\frac12 mv^2=\frac12 v^2=\frac12 v^2$ ,

and this must equal the potential energy $\text{PE}_0$ :

$\frac{8}{9}g^2=\frac12 v^2\Rightarrow v=\frac43g$ .

Now this is where things get trickier. My idea was to use conservation of momentum on the two particles separately. As this clever answer to this question shows, you can treat the 5 kg mass, string, and 1 kg mass as a single particle.

So the prior momentum is the mass of the 1 kg mass by $\frac43 g$ :

$p_0=m_0u=1\cdot \frac43 g=\frac43g$ .

The ‘after’ momentum is the mass of the 1 kg and 5 kg masses times the new velocity:

$p_1=m_1v=6\cdot v$ .

By Conservation of Momentum, these are equal:

$\frac43 g=6v\Rightarrow v=\frac{2}{9} g\text{ m s}^{-1}$ .

Leaving Cert Applied Maths, 1995 Q. 5 (a)

November 13, 2017 in Leaving Cert Applied Maths | Leave a comment

The following question gave a little grief:

Two smooth spheres of masses $2m$ and $3m$ respectively lie on a smooth horizontal table.

The spheres are projected towards each other with speeds $4u$ and $u$ respectively.

i. Find the speed of each sphere after the collision in terms of $e$ , the coefficient of restitution

ii. Show that the spheres will move in opposite directions after the collision if $e>\frac13$ .

My contention is that the question erred in not specifying that the answers to part i. were to be in terms of $e$ and $u$ .

Solution:

i. The following is the situation:

diagram

Let $v_1$ and $v_2$ be the velocities of the smaller respectively larger sphere after collision. Note that the initial velocity of the larger sphere is minus $u$ .

Using conservation of momentum,

$m_1u_1+m_2u_2=m_1v_1+m_2v_2$

$\Rightarrow 2m(4u)+3m(-u)=2mv_1+3mv_2$

$\Rightarrow 5u=2v_1+3v_2$ .

Using:

$\displaystyle e(u_1-u_2)=-(v_1-v_2)\Rightarrow \frac{v_1-v_2}{u_1-u_2}=-e$ ,

Therefore,

$\displaystyle \frac{v_1-v_2}{4u-(-u)}=-e$

$\Rightarrow v_1-v_2=-5ue\Rightarrow v_1=v_2-5ue$ ,

and so

$5u=2(v_2-5ue)+3v_2\Rightarrow 5u=2v_2-10ue+3v_2$ ,

$\Rightarrow 5v_2=5u+10ue\Rightarrow v_2=u(1+2e)$ .

$\Rightarrow v_1=u(1+2e)-5ue=u+2ue-5ue=u(1-3e)$ .

ii. $v_2>0$ . If $e>\frac13\Rightarrow 3e>1\Rightarrow 1-3e<0$ and so

$v_1=u(1-3e)<0$ ;

that is the particles move in opposite directions.

	J.P. McCarthy on MATH6040: Spring 2022, Week…
	J.P. McCarthy on MATH6040: Spring 2022, Week…
	J.P. McCarthy on MATH7019: Winter 2020, Week…
	J.P. McCarthy on MATH7019: Winter 2020, Week…
	A Sufficient Conditi… on Almost All Trees have Quantum…

Category Archive

Boxroom Mathematics: Episode I

Difficult Connected Particles Question

Question (a)

(i)

Solution

Another Relative Velocity Question

Solution:

Relative Velocity Question Three Ways

LCHL 2007, Q. 2(a)

Vector Approach to (ii)

On Parallel and Perpendicular Lines

Lines

Exercise:

The Equation of a Line

Some Leaving Cert Applied Maths Notes

The Line of Best Fit

Direct Proportion

Writing a Cosine Plus Sine as a Sine

$a\cdot \cos\theta- b\cdot\sin\theta$

The Principle of Conservation of Momentum for Pulleys

Leaving Cert Applied Maths, 1995 Q. 5 (a)

Recent Comments

Categories

J.P. McCarthy Maths

Category Archive

Share this:

Like this:

Question (a)

(i)

Solution

Share this:

Like this:

Solution:

Share this:

Like this:

LCHL 2007, Q. 2(a)

Vector Approach to (ii)

Share this:

Like this:

Lines

Exercise:

The Equation of a Line

Share this:

Like this:

Share this:

Like this:

Direct Proportion

Share this:

Like this:

Share this:

Like this:

Share this:

Like this:

Share this:

Like this:

Recent Comments

Categories