In theory (see Learner Workload) you are supposed to spend seven hours per week on MATH6040. I know this might not be possible for everyone, but there is no doubt that spending four hours per week on exercises is going to be best for your learning. Any questions, please email.
Test 1 – Week 5
Please see Canvas —> MATH6040 —> Assignments for more information.
Week 3
Lecture
In Week 3 we finished Chapter 1, and the material for Test 1, by talking at the applications of vectors to work and moments
We had an hour and a half of tutorial time on the p.47 and p.40 Exercises.
Exercises
How much time you put into homework is up to you: of course the more time you put in the better but we all have competing interests. Please feel free to ask me questions about the exercises:
- Sample Test 1, p.56-61 (gives an idea of layout and length only)
- p. 47, Q.1-6
There is an applet to play with:
Additional questions include:
- p. 49, Q.7-14
There are more questions to be found in Weeks 1 and 2.
Additional practise questions (beyond the manual) may be found by looking at past MATH6040 exam papers.
Week 4
We will start at 19:05 with a Vectors Concept MCQ.
We will start looking at Chapter 2: Matrices. We will some examples of matrix arithmetic and look at Matrix Inverses — “dividing” for Matrices. This will allow us to solve matrix equations.
We will likely have no tutorial time.
Study
Please feel free to ask me questions about the exercises via email.
Student Resources
Please see Student Resources for information on the Academic Learning Centre, etc.
J.P. McCarthy: Math Page 
2 comments
Comments feed for this article
February 14, 2022 at 8:36 am
J.P. McCarthy
Re: p.49, Q.6
The force is of magnitude 12 in the direction of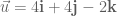
. The magnitude of 
is 
.
Therefore:
.
Alternatively, find
and:
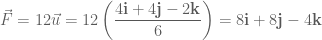
Regards,
J.P.
February 14, 2022 at 8:50 am
J.P. McCarthy
Re: Sample Test 1, Q.3
There are two issues with your solution. You would receive a minimal penalty for the first thing, and some of the marks lost in the second issue would be reclaimed by the way you checked your answer (just write on test that you know there is a mistake).
1. The first right-done-diagonal should be
. Look again.
2. It is probably safer to multiply the whole way along the diagonals, so you also multiply as appropriate by the vectors
.
So you would get rather:
which is equal to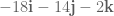
.
To do what you are doing you must be more careful and have:
I think you are better off going with the approach above.
Regards,
J.P.