Category Archive

You are currently browsing the category archive for the ‘Research’ category.

An approach to the maximality conjecture for quantum permutation groups

April 4, 2024 in C*-Algebras & Operator Theory, Quantum Groups, Research | Leave a comment

The following is an approach to the maximality conjecture for $S_N\subset S_N^+$ which asks what happens to a counterexample $S_N\subsetneq \mathbb{G}_N\subsetneq S_N^+$ when you quotient $C(\mathbb{G}_N)\to C(\mathbb{G}_N)/\langle 1-u_{NN}\rangle$ . If $C(\mathbb{G}_N)/\langle 1-u_{NN}\rangle$ is noncommutative, you generate another counterexample $S_{N-1}\subsetneq \mathbb{G}_{N-1}\subsetneq S_{N-1}^+$ .}

Most of my attempts at using this approach were doomed to fail as I explain below.

Let $\mathbb{G}\subseteq S_N^+$ be a quantum permutation group with (universal) algebra of continuous functions $C(\mathbb{G})$ generated by a fundamental magic representation $u\in M_N(C(\mathbb{G}))$ . Say that $\mathbb{G}$ is classical when $C(\mathbb{G})$ is commutative and genuinely quantum when $C(\mathbb{G})$ is noncommutative.

Definition 1 (Commutator and Isotropy Ideals)

Given $\mathbb{G}\subseteq S_N^+$ , the commutator ideal $J_N\subset C(\mathbb{G})$ is given by:

$\displaystyle J_N=\langle [u_{ij},u_{kl}]\,\mid\, 1\leq i,j,k,l\leq N\rangle.$

The isotropy ideal $I_N\subset C(\mathbb{G})$ is given by:

$\displaystyle I_N=\langle 1-u_{NN}\rangle.$

Lemma 1

The commutator ideal $J_N\subset C(\mathbb{G})$ is equal to the ideal

$\displaystyle K_N:=\langle u_{i_1j_1}u_{i_2j_2}u_{i_1j_3},u_{i_1j_1}u_{i_2j_2}u_{i_3j_1}\,\mid \, 1\leq i_k,j_k\leq N,\,j_1\neq j_3,i_1\neq i_3\rangle.$

Proof:

$\begin{aligned} [u_{i_2j_2},u_{i_3j_1}] & =u_{i_2j_2}u_{i_3j_1}-u_{i_3j_1}u_{i_2j_2} \\ \implies u_{i_1j_1}[u_{i_2j_2},u_{i_3j_1}] & = u_{i_1j_1}u_{i_2j_2}u_{i_3j_1}\qquad (i_1\neq i_3)\\ \implies u_{i_1j_1}u_{i_2j_2}u_{i_3j_1} & \in J_N, \end{aligned}$
with a similar statement for $u_{i_1j_1}u_{i_2j_2}u_{i_1j_3}$ .

On the other hand:
$\begin{aligned} [u_{i_1j_1},u_{i_2j_2}] & =u_{i_1j_1}u_{i_2j_2}-u_{i_2j_2}u_{i_1j_1} \\ & =u_{i_1j_1}u_{i_2j_2}\sum_{k=1}^Nu_{i_1k}-\sum_{l=1}^{N}u_{i_1l}u_{i_2j_2}u_{i_1j_1} \\ & = u_{i_1j_1}u_{i_2j_2}u_{i_1j_1}+u_{i_1j_1}u_{i_2j_2}\sum_{k\neq j_1}u_{i_1j_1}u_{i_2j_2}u_{i_1k}-\\&u_{i_1j_1}u_{i_2j_2}u_{i_1j_1}\sum_{l\neq j_1}u_{i_1l}u_{i_2j_2}u_{i_1j_1}\\ \implies [u_{i_1j_1},u_{i_2j_2}]& \in K_N \end{aligned}$

Proposition 1

The commutator and isotropy ideals are Hopf*-ideals. The quotient $C(\mathbb{G})\to C(\mathbb{G})/J_N$ gives a classical permutation group $G\subset S_N$ , the classical version $G\subseteq \mathbb{G}$ , and the quotient $C(\mathbb{G})\to C(\mathbb{G})/I_N$ giving an isotropy quantum subgroup. If $\mathbb{G}$ is classical, this quotient is the isotropy subgroup of $N$ for the action $\mathbb{G}\curvearrowright {1,2,\dots,N}$ .

Via $C(S_N^+)\to C(S_N^+)/J_N$ , the classical permutation group is a quantum subgroup $S_N\subset S_N^+$ . It is conjectured that for all $N$ it is a maximal subgroup.

Theorem 1 (Wang/Banica/Bichon)

$S_N\subseteq S_N^+$ is maximal for $1\leq N\leq 5$ .

Read the rest of this entry »

On the number of fixed points of conditioned quantum permutations

March 31, 2024 in Probability Theory, Quantum Groups, Research | Leave a comment

Consider the symmetric group $S_N$ . Let $\mathrm{fix}_N \in C(S_N)$ count the number of fixed points of a permutation $\sigma\in S_N$ . Where $X\sim \mathrm{Poi}[1]$ , we have that for a random permutation $\xi_N\in S_N$ chosen with respect to the uniform distribution, the $\mathrm{fix}_N$ converges in distribution to $X$ in the sense that:

$\displaystyle \lim_{N\to \infty}\mathbb{P}[\mathrm{fix}_N(\xi_N)=m]=\mathbb{P}[X=m]$ .

In this note we will look at the distribution in the case where the uniform distribution is conditioned on $\xi_N(1)=1$ .

Theorem

Let $\xi_N\in S_N$ be chosen according to the distribution uniform on permutations for which one is a fixed point. The number of fixed points has distribution $1+\mathrm{Poi}[1]$ in the sense that, where $X\sim \mathrm{Poi}[1]$ ,

$\displaystyle \lim_{N\to \infty}\mathbb{P}[\mathrm{fix}_N(\xi_N)=m]=\mathbb{P}[X=m-1]$ .

Proof: What can be shown, ostensibly from stuff from the quantum permutation side of the house is that, where $h_N$ is integration against the uniform distribution, and $\widetilde{h_N}$ is integration against the uniform distribution on permutations with one a fixed point, that, for $k<N$ :

$\displaystyle \widetilde{h_N}(\mathrm{fix}_N^k)=h_N(\mathrm{fix}_N^{k+1})=B_{k+1}$ ,

the $(k+1)$ -st Bell number. Now consider the moments of $1+X$ :

$\displaystyle \sum_{t=0}^\infty t^k\mathbb{P}[1+X=t]=\sum_{t=0}^\infty t^k\mathbb{P}[X=t-1]$

$\displaystyle =\sum_{t=1}^\infty t^k\frac{e^{-1}}{(t-1)!}$

$\displaystyle \underset{s=t-1}{=}\sum_{s=0}^\infty(s+1)^k\frac{e^{-1}}{s!}$

$\displaystyle =\sum_{s=0}^\infty\sum_{i=0}^k\binom{k}{i}s^i \frac{e^{-1}}{s!}$

$\displaystyle =\sum_{i=0}^k\binom{k}{i}\sum_{s=0}^\infty s^i\frac{e^{-1}}{s!}$

$\displaystyle =\sum_{i=0}^k \binom{k}{i} B_k=B_{k+1}$ ,

using the fact that the Bell numbers are the moments of that Poisson distribution and the standard recurrence for the Bell numbers.

Local vs Global Conditioning of Quantum Permutations

In the quantum case we define

$\displaystyle \mathrm{fix}_N:=\mathrm{Tr}(u)$ ,

where $u\in M_N(C(S_N^+))$ is the fundamental magic representation. The moments of $\mathrm{fix}_N$ with respect to the Haar state are the Catalan numbers and it follows that the law of $\mathrm{fix}_N$ is a Marchenko-Pastur distribution, with density

$\displaystyle \dfrac{1}{2\pi}\sqrt{\frac{4}{t}-1}$ :

Note that when we measure the Haar state with some finite spectrum version of $\mathrm{fix}_N$ we find:

the probability of finding an integer number of fixed points is zero, and
independently of $N$ , the probability of finding more than four fixed points is zero.

In the classical case above when we chose the permutation uniformly from those who fix one, there are two ways of viewing it:

we pick an element of $S_N$ that fixes one, OR
we consider the isotropy subgroup $S_{N-1}\subset S_N$ and choose our permutation from $S_{N-1}$ .

Classically, these are the same thing. In the quantum case these two things can be interpreted differently. The second case is quite clear in the quantum case. For $N>4$ , we take the isotropy $S_{N-1}^+\subset S_N^+$ via the quotient $C(S_N^+)\to C(S_N^+)/\langle1-u_{11}\rangle$ .

The analogue of the uniform distribution on $S_{N-1}\subset S_N$ here is the Haar idempotent $h_{C(S_{N-1}^+)}\circ \pi$ . Note this maps $\mathrm{fix}_N$ to $1+\mathrm{fix}_{N-1}$ . Now, using the fact that $h_{C(S_{N-1}^+)}(\mathrm{fix}_{N-1})=C_k$ , the Catalan number, we have that the moments of $\mathrm{fix}_N$ with respect to $h_{C(S_{N-1}^+)}\circ \pi$ is the binomial transform of the Catalan numbers (the binomial transform of $B_1,\dots,B_k$ is $B_{k+1}$ ). It follows, using similar stuff to the above, that the distribution of $\mathrm{fix}_N$ with respect to $h_{C(S_{N-1}^+)}\circ \pi$ is just a shifted version of Marchenko–Pastur:

I guess this is marginally more interesting than the unshifted version.

Now, what about an analogue of “we pick an element of $S_N$ that fixes one”. So if we take the Haar state and measure the observable $u_{11}\in C(S_N^+)$ that asks of a quantum permutation, does it fix one, we get, conditioned on this, the state:

$\displaystyle h_1(f):=N\cdot h(u_{11}fh_{11})=\dfrac{h(u_{11}fu_{11})}{h(u_{11})}\qquad (f\in C(S_N^+))$ .

And, it turns out, as above, using stuff from the quantum permutation side of the house:

$\displaystyle h_1(\mathrm{fix}_N^k)=h(\mathrm{fix}_N^{k+1})=C_{k+1}$ .

Quite quickly from here we find that the density of the distribution of $\mathrm{fix}_N$ with respect to $h_1$ is

$\displaystyle \frac{t}{2\pi}\sqrt{\frac{4}{t}-1}$

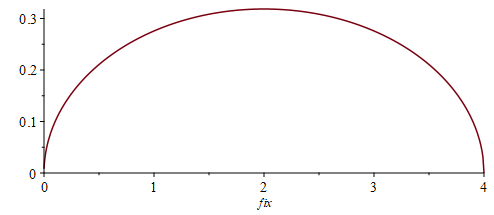
This is so interesting:

it doesn’t change the support — we still find between 0 and 4 fixed points,
we have a new symmetry about $\mathrm{fix}_N=2$ , we had another unexpected symmetry here.
the mean jumps from one to two, that is not unexpected, but
the mode jumps from zero to two!
even though we have observed one to one, there can still be less than one fixed point when we measure… and this happens with probability $\approx 1/5$ .

The next obvious question is what happens with:

$\displaystyle f\mapsto \dfrac{h_1(u_{22}fu_{22})}{h_1(u_{22})}\qquad (f\in C(S_N^+))$

Epilogue?

So what about this local vs global conditioning? Well, no matter what subsequent measurements are made to $h_{C(S_{N-1}^+)}\circ \pi$ , we will always find that one is a fixed point. That conditioning is ‘global’.

This is not the case with $h_1$ , and why the support of the law is not bounded above one, like that of the globally conditioned $h_{C(S_{N-1}^+)}\circ \pi$ . In fact, there is a non-zero probability that $h_1$ is observed to fix two but then subsequently not fix one anymore. That conditioning was only local: the probability that $h_1$ fixes one is 100%… but subsequent measurements can destroy that conditioning… it is only local.

A strange property of quantum permutations

February 13, 2024 in Probability Theory, Quantum Groups, Research | Leave a comment

Classical Warm-up

Let $S_N$ be the classical permutation group on $N$ symbols. The algebra of continuous functions $C(S_N)$ on $S_N$ is generated by indicator functions:

$\displaystyle \mathbf{1}_{j\to i}(\sigma)=\delta_{i,\sigma(j)}$ .

This algebra is commutative, but we will use some non-commutative algebraic analogues. Let $\widetilde{\pi}\in M_p(S_N)$ be the uniform probability distribution on $S_N$ and by $\pi$ the associated state on $C(S_N)$ :

$\displaystyle\pi(f)=\sum_{t\in G}f(t)\,\widetilde{\pi}(\{t\})=\frac{1}{|S_N|}\sum_{t\in G} f(t)\qquad (f\in C(S_N))$

When choosing a permutation at random what is the probability that it sends $1\to 1$ ? Well, this will equal, in some notation we won’t fully explain here:

$\displaystyle \mathbb{P}[\pi(1)=1]=\pi(\mathbf{1}_{1\to 1})=\frac{1}{N}$ .

Once this has been observed, there is a conditioning of the state $\pi\mapsto \pi_{1\to 1}$ :

$\displaystyle \pi_{1\to 1}(f)=\dfrac{\pi(\mathbf{1}_{1\to 1}f\mathbf{1}_{1\to 1} )}{\pi(\mathbf{1}_{1\to 1})}=N \pi(\mathbf{1}_{1\to 1}f\mathbf{1}_{1\to 1} )) \qquad (f\in C(S_N))$ .

The state was given by $\pi$ but is now given by $\pi_{1\to 1}$ . Now, after having observed this random permutation mapping $1\to 1$ , we can ask it another question.

Consider a subset $S\subseteq \{3,\dots,N\}$ and define:

$\displaystyle\mathbf{1}_{3\to S}:=\sum_{s\in S}\mathbf{1}_{3\to s}$ .

This is an observable, which basically asks of a permutation, do you map three into $S$ ? One for yes, zero for no. So let us ask this of $\pi_{1\to 1}$ :

What is the probability that a random permutation maps three into $S$ after having been observed mapping one to one?

We find, with a fairly elementary calculation that the answer to this question is:

$\displaystyle \mathbb{P}[\pi_{1\to 1}(3)\in S]=\frac{|S|}{N-1}$ .

If $\pi_{1\to 1}(3)\in S$ , we get further conditioning, to let us say $\nu$ :

$\displaystyle \nu(f)=\frac{N(N-1)}{|S|}\pi(\mathbf{1}_{1\to 1}\mathbf{1}_{3\to S}f\mathbf{1}_{3\to S}\mathbf{1}_{1\to 1})\qquad (f\in C(S_N))$

What is the probability that after seeing $\pi_{1\to 1}(3)\in S$ after $\pi(1)=1$ we see $\nu(2)=2$ ? We find it is:

$\displaystyle \mathbb{P}[\nu(2)=2]=\frac{1}{N-2}$ .

Therefore, where $\succ$ means after, and the state-conditioning implicit

$\displaystyle \mathbb{P}[(\pi(2)=2)\succ (\pi(3)\in S)\succ(\pi(1)=1)]$

$\displaystyle =\frac{1}{N}\cdot \frac{|S|}{N-1}\cdot\frac{1}{N-2}=\frac{|S|}{N(N-1)(N-2)}$

Now let us ask a ridiculous question. What was the probability that $\nu(1)=2$ ? But $\nu$ is just a conditioning of $\pi_{1\to 1}$ , which mapped one to one with probability one:

$\displaystyle \mathbb{P}[\pi_{1\to 1}(1)=1]=\dfrac{\pi(\mathbf{1}_{1\to 1}\mathbf{1}_{1\to 1}\mathbf{1}_{1\to 1})}{\pi(\mathbf{1}_{1\to 1})}=1$ .

Of course the answer is zero. Can we actually see it in the above framework: well, yes, because the algebra of functions is commutative. You end up with evaluating a state at

$\displaystyle \mathbf{1}_{1\to 1}\mathbf{1}_{3\to S}\mathbf{1}_{1\to 2}\mathbf{1}_{3\to S}\mathbf{1}_{1\to 1}$ ,

but commutativity sees $\mathbf{1}_{1\to 1}\mathbf{1}_{1\to 2}$ … and no permutation maps one to one and one to two (you’d need a relation to do that), and so $\mathbf{1}_{1\to 1}\mathbf{1}_{1\to 2}=0$ , so is the length five monomial above, and so is the probability we spoke about.

We don’t have to do state conditioning and multiplication to calculate the probability that a random permutation maps one to one, then maps three into $S$ , then maps two to two though. Where $|f|^2=f^*f$ :

$\displaystyle \mathbb{P}[(\pi(2)=2)\succ (\pi(3)\in S)\succ(\pi(1)=1)]$

$=\pi(|\mathbf{1}_{2\to 2}\mathbf{1}_{3\to S}\mathbf{1}_{1\to 1}|^2)=\dfrac{|S|}{N(N-1)(N-2)}$ .

Let us remark that this probability is increasing in $|S|\in\{0,1,\dots,N-2\}$ : the less we specify about the event, in this case represented by the projection $\mathbf{1}_{3\to S}$ , the more general it is, the larger the probability.

Let’s Go Quantum

In the case of quantum permutations, so talking $S_N^+$ the ridiculous question of asking what is the probability that a quantum permutation maps one to two after it had previously mapped one to one… is no longer zero. Where $q(N)=N(N-1)(N^2-4N+2)$ , the probability of the analogue of a “random” quantum permutation, the Haar state $h$ doing this is:

$\displaystyle \mathbb{P}[(h(1)=2)\succ(h(3)=3)\succ (h(1=1))]=\frac{N-3}{q(N)}$

Anyway, the quantum versions of the $\mathbf{1}_{j\to i}$ are entries $u_{ij}\in M_N(C(S_N^+))$ of a universal magic unitary. We say:

$\mathbb{P}[(h(2)=2)\succ (h(3)\in S)\succ (h(1)=1)]:=h(|u_{22}u_{S,3}u_{11}|^2)$ ,

where $u_{S,3}=\sum_{s\in S}u_{s3}$ . We find this probability is:

$\displaystyle \mathbb{P}[(h(2)=2)\succ (h(3)\in S)\succ (h(1)=1)]=\frac{|S|(N^2-5N+5+|S|)}{(N-2)q(N)}$ .

This is also increasing in $|S|$ . Again, the less specificity about the event, the greater the probability.

This quantity is related to the classical probability above, and there are asymptotic similarities. Writing $|S|=N-2-|S^c|$ , where $S^c$ is the complement of $S$ in $\{3,4,\dots,N\}$ :

$\displaystyle \mathbb{P}[(h(2)=2)\succ (h(3)\in S)\succ (h(1)=1)]$

$\displaystyle=\mathbb{P}[(\pi(2)=2)\succ (\pi(3)\in S)\succ(\pi(1)=1)]\cdot\left[1-\frac{|S^c|+1}{q(N)}\right]$

I guess this also says, the larger $|S|$ , the more similar the classical and quantum probabilities.

A twist

What if instead of looking at $h(2)=2$ after $h(3)\in S$ after $h(1)=1$ but instead we asked about $h(1)=2$ ? This should be non-zero, but what is the dependence on $|S|$ ?

From our classical intuition, we would probably just expect, well, the same really. The larger the value of $|S|$ , the less we are saying about the event. The larger the probability. But in fact this is not the case. The probability is largest when $|S|$ is close to $(N-2)/2$ . We will write down the probability, and then explain, mathematically, why the symmetry with respect to $|S|\leftrightarrow N-2-|S|$ , with respect to $S\leftrightarrow S^c$ :

$\displaystyle \mathbb{P}[(h(1)=2)\succ (h(3)\in S)\succ (h(1)=1)]=\dfrac{|S|(N-2-|S|)}{q(N)}$ .

Proof: Consider $u_{21}u_{11}=0$ . Insert between them $1_{C(S_N^+)}=\sum_{k=1}^Nu_{k3}$ :

$\displaystyle u_{21}\sum_{k=1}^Nu_{k3} u_{11}=\sum_{k=1}u_{21}u_{k3}u_{11}=0$ .

Like in the classical case, by definition here, $u_{21}u_{23}=0=u_{13}u_{11}=0$ . So split into two sums:

$\displaystyle \sum_{s\in S}u_{21}u_{i3}u_{11}+\sum_{j\in S^c}u_{21}u_{j3}u_{11}=0$ .

Now, classically, this is just a sum of zero terms equal to zero, but not in the quantum world where we have these $u_{21}u_{j3}u_{11}\neq 0$ . They are not positive though. We can now split:

$\displaystyle \sum_{s\in S}u_{21}u_{i3}u_{11}=-\sum_{j\in S^c}u_{21}u_{j3}u_{11}$ .

Now take the $|\cdot|^2$ of both sides to show that:

$\displaystyle |u_{21}u_{S,3}u_{11}|^2=|u_{21}u_{S^c,3}u_{11}|^2$

This yields the strange probability above. I think any intuition I have for this would be very much post-hoc. I think I will just let it hang there as something weird, cool and mysterious about quantum permutations…

An interesting addend to Tracing the orbitals of the quantum permutation group

February 6, 2024 in C*-Algebras & Operator Theory, Quantum Groups, Research | Leave a comment

This paper referenced in the title (preprint here) tries to establish some very basic properties of a so-called exotic quantum permutation group, one intermediate to the classical and quantum permutation groups:

$\displaystyle S_N\subsetneq \mathbb{G}\subsetneq S_N^+$ .

If a compact matrix quantum subgroup $\mathbb{H}\subseteq \mathbb{G}$ (here $\mathbb{G}$ is generic, not exotic) given by a quotient $\pi:C(\mathbb{G})\to C(\mathbb{H})$ , is such that for all monomials $f$ in the generators $u_{ij}\in C(\mathbb{G})$ :

$\displaystyle h_{C(\mathbb{H})}(\pi(f))=h_{C(\mathbb{G})}(f)$ ,

then in fact $\mathbb{H}=\mathbb{G}$ . In the paper above I explored calculating the Haar state on $C(S_N^+)$ using invariances related to the inclusion $S_N\subseteq S_N^+$ … the point being that the Haar measure on exotic $\mathbb{G}$ shares these invariances too… and perhaps, very speculatively, we could show that these Haar states coincide on such monomials… and a famous open problem in the theory would be solved.

The paper above fails at generators of length four though. The invariances do not determine the Haar measure on $S_N^+$ and we have to include a representation theory result around the law of the main character to give the explicit formulae. If we leave out the representation theory input, we have the Haar state up to a parameter.

However, a very basic algebraic result, that a product of three generators in exotic $C(\mathbb{G})$ can be zero for trivial reasons only, allows us to put bounds on the Haar state. If these bounds could force the fourth moment of the main character (with respect to the Haar state) to equal 14, then the Haar state on length four monomials would be equal for both. Alas… they only bound them less than or equal to 15. At this point the paper gives up… but this moment is a whole number, either 14 or 15… so I added the relation that the fourth moment is 15… and what comes out is that the parameter above is zero… but when this parameter is zero we find, in exotic $\mathbb{G}$ :

$\displaystyle h(|u_{22}u_{11}u_{23}|^2)=0$ ,

but this is not the case, as $u_{22}u_{11}u_{23}$ is not zero for trivial reasons, and the Haar state is faithful… the fourth moment equal to 15 gives classical $S_N\subseteq S_N^+$ . Therefore the fourth moment for exotic $\mathbb{G}\subset S_N^+$ is forced equal to 14, giving the same explicit formula for length four generators as for $S_N^+$ . Further work needed here.

A note on universal C*-algebras

February 2, 2024 in C*-Algebras & Operator Theory, Quantum Groups, Research | Leave a comment

Idea and Intuition

Let $\mathcal{G}=\{g_i\}_{i\geq 1}$ be a (usually finite) set of generators and $\mathcal{R}$ a (usually finite) set of relations between the generators. The generators at this point are indeterminates, and we will be momentarily vague about what is and isn’t a relation. We write (if it exists!) $\mathrm{C}^*(\mathcal{G}\mid \mathcal{R})$ for the universal $\mathrm{C}^*$ -algebra generated by generators $\mathcal{G}$ and relations $\mathcal{R}$ .

It has the following universal property. Suppose $|\mathcal{G}|=n$ . Let $A$ be a $\mathrm{C}^*$ -algebra with elements $f_1,\dots,f_n$ that satisfy the relations $\mathcal{R}$ , then there is a (unique) *-homomorphism $\mathrm{C}^*(\mathcal{G}\mid\mathcal{R})\to A$ mapping $g_i\mapsto f_i$ . This map will be a surjective *-homomorphism $\mathrm{C}^*(\mathcal{G}\mid\mathcal{R})\to \mathrm{C}^*(f_1,\dots,f_n)$ (aka a quotient map and $\mathrm{C}^*(f_1,\dots,f_n)$ a quotient of $\mathrm{C}^*(\mathcal{G}\mid\mathcal{R}))$ .

If the $f_i\in A$ generate $A$ , $\mathrm{C}^*(f_1,\dots,f_n)$ , then $\mathrm{C}^*(\mathcal{G}\mid\mathcal{R})\to A$ is a surjective *-homomorphism.

My (highly non-rigourous, the tilde reminding of hand-waving) intuition for this object is that you collect all (really all, not just isomorphism classes, we want below $C([0,1])$ and e.g. $C([0,2]$ ) of $\mathrm{C}^*$ -algebras $A_\lambda$ generated by $n$ generators satisfying the relations $\mathcal{R}$ and forming a “big direct sum/product thingy” out of all of them:

$\displaystyle \mathrm{C}^*(\mathcal{G}\mid\mathcal{R})\sim \widetilde{\prod_{\lambda\in \Lambda}}A_\lambda$ .

Then the *-homomorphism $\pi_\mu:A\to A_\mu$ given by the universal property is given by projection onto that factor (which is a surjective *-homomorphism, a quotient):

$\displaystyle\pi_\mu:\widetilde{\prod_{\lambda\in \Lambda}}A_\lambda\to A_\mu$ .

This intuition works well but we should give a brief account of things are done properly.

First off, not every relation will give a universal $\mathrm{C}^*$ -algebra. For example, consider $\mathcal{G}=\{g\}$ and $\mathcal{R}=\{g=g^*\}$ . The problem here is one of norm. Recall our rough intuition from above. What is the norm on $a\in \mathrm{C}^*(\mathcal{G}\mid\mathcal{R})$ , this big thing $\widetilde{\prod_{\lambda\in\Lambda}}A_\lambda$ ? It should be something like, where the norm of $A_\lambda$ is $\|\cdot\|_\lambda$ the supremum over the factors:

$\displaystyle \|f\|\sim\sup_{\lambda\in \Lambda}\|\pi_{\lambda}(f)\|_{\lambda}\qquad (f\in \mathrm{C}^*(\mathcal{G}\mid\mathcal{R})).$

The first approach to show that $\mathrm{C}^*(g\mid g=g^*)$ does not exist is to consider for each $\alpha\in [0,\infty)$ the $\mathrm{C}^*$ -algebra $A_\alpha=C([0,\alpha])$ which is singly-generated by the self-adjoint $f_\alpha:=t\mapsto t$ . But the norm $\|\cdot \|_\alpha$ in $A_\alpha$ is the supremum norm, so we find $\|f_\alpha\|_{\alpha}=\alpha$ . From here:

$\displaystyle \|g\|\sim\sup_{\lambda\in \Lambda}\|\pi_{\lambda}(g)\|_{\lambda}\geq \sup_{\alpha\in [0,\infty)}\|f_{\alpha}\|_{\alpha}=\sup_{\alpha\in [0,\infty)}\alpha,$

which is unbounded. The relations must give a bounded norm to the generators.

As an example of relations that do bound the generators, consider, $n$ self-adjoint generators such that the sum of their squares is the identity:

$\displaystyle \mathrm{C}^*\left(g_1,\dots,g_n\mid g_i=g_i^*,\,\sum_i g_i^2=1\right)$ .

These relations bounds the norm of the generators $\|g_i\|\leq 1$ ¹, and this gives existence to this algebra, using the Gelfand philosophy giving the “algebra of continuous functions on the free sphere”, $C(\mathcal{S}^{n-1}_+)$ (I think first considered by Banica and Goswami).

Note here the relations are given by polynomial relations. If the polynomial relations are suitably admissible (i.e. give a bound to the generators), in this setting there is a real construction (real vs our ridiculous $\widetilde{\prod}$ ) of $\mathrm{C}^*(\mathcal{G}\mid\mathcal{R})$ . See p.885 (link to *.pdf quantum group lecture notes of Moritz Weber).

In fact, this is only a small class of the possible relations. I suggest there are at least two more types:

$\mathrm{C}^*$ relations that would be (admissible) norm relations (for example, in one generator, adding $\|g\|\leq 1$ , a non-polynomial relation, to the polynomial relation $g=g^*$ gives an admissible set of relations, and $\mathrm{C}^*(g\mid g=g^*,\|g\|\leq 1)\cong C([-1,1])$ . For $\mathrm{C}^*$ /norm relations see here and maybe here.
(admissible) strong relations (see here for a use of this, with reference)

The constructions in one or both of cases might be constructive, as in the case (admissible) polynomial relations, but there is also an approach using category theory. But the main feature in all such definitions is the universal property, whose use could be summarised as follows:

Let $\mathrm{C}^*(\mathcal{G}\mid\mathcal{R})$ be a universal $\mathrm{C}^*$ -algebra. The universal property can be used to answer questions about $\mathrm{C}^*(\mathcal{G}\mid\mathcal{R})$ such as:

is some polynomial $p(g_1,\dots,g_n)$ in the generators non-zero,

is $\mathrm{C}^*(\mathcal{G}\mid\mathcal{R})$ infinite dimensional,

is $\mathrm{C}^*(\mathcal{G}\mid\mathcal{R})$ non-commutative;

because, if $A$ is a $\mathrm{C}^*$ -algebra with elements $f_1,\dots,f_n$ that satisfy the relations then there is a unique *-homomorphism $\pi:\mathrm{C}^*(\mathcal{G}\mid\mathcal{R})\to \mathrm{C}^*(f_1,\dots,f_n)$ . So, for example, where $B$ is some such $\mathrm{C}^*(f_1,\dots,f_n)$ then

if $p(f_1,\dots,f_n)\neq 0$ , then $p(g_1,\dots,g_n)\neq 0$ as $\pi(p(g_1,\dots,g_n))=p(f_1,\dots,f_n)$ ,

if $B$ is infinite dimensional then $\pi$ is a surjective *-homomorphism onto an infinite dimensional algebra, and so the domain $\mathrm{C}^*(\mathcal{G}\mid\mathcal{R})$ is infinite dimensional too.

if the commutator $[f_i,f_j]\neq 0$ , so that $B$ is non-commutative, then so is $\mathrm{C}^*(\mathcal{G}\mid\mathcal{R})$ as $\pi([g_i,g_j])=[f_i,f_j]$

These quotients $B$ can be considered models of $\mathrm{C}^*(\mathcal{G}\mid\mathcal{R})$ .

Two Examples

A projection $p$ in a $\mathrm{C}^*$ -algebra is such that $p=p^2=p^*$ . Consider

$A:=\mathrm{C}^*(p,q,1\mid p\text{ and }q\text{ are projections})$ .

Existence is easy, because the norm of a non-zero projection is one. To answer questions about this algebra consider the infinite dihedral group $D_\infty=\langle a,b\mid a^2=b^2=e\rangle$ . This has group algebra $\mathbb{C}D_\infty$ and group $\mathrm{C}^*$ -algebra $\mathrm{C}^*(D_\infty)$ . Note that $a$ and $b$ in $\mathrm{C}^*(D_\infty)$ satisfy the relations of $A$ , and so we have a *-homomorphism (in fact a *-isomorphism) $\pi:A\to \mathrm{C}^*(D_\infty)$ . This tells us that any monomial in the generators of $A$ is non-zero, $A$ is infinite dimensional, and $A$ is non-commutative.

A partition of unity is a finite set of projections that sum to the identity, $\sum_{i}p_i=1$ . A magic unitary in a $\mathrm{C}^*$ -algebra $A$ is a matrix $u\in M_N(A)$ such that the entries along any one row or column form a partition of unity. Consider (notation to be kept mysterious):

$\displaystyle C(S_N^+)=\mathrm{C}^*\left(u_{ij}\mid u\text{ an }N\times N\text{ magic unitary}\right)$ .

Consider the following magic unitary:

$\displaystyle v=\begin{bmatrix}p & 1-p & 0 & 0 \\ 1-p & p & 0 & 0 \\ 0 & 0 & q & 1-q \\ 0 & 0 & 1-q & q\end{bmatrix}$ .

Note that the $v_{ij}$ satisfy the relations of $C(S_N^+)$ and in fact generate $A=\mathrm{C}^*(p,q)$ from above. Thus we have a quotient $\pi:C(S_4^+)\to A$ which shows that $C(S_4^+)$ is infinite dimensional and noncommutative.

It is possible to show using a magic unitary with entries in $M_N(\mathbb{C})$ that for $N>3$ , a monomial with entries in $u\in M_N(C(S_N^+))$ is zero for trivial reasons only (link to *.pdf, from Theorem 1 on).

In addition it can be shown that for $u$ (and similarly $v$ ) the matrix in $M_N(C(S_N^+)\otimes_{\min} C(S_N^+))$ with $(i,j)$ – entries

$\displaystyle \sum_{k=1}^Nu_{ik}\otimes u_{kj}$

is a magic unitary, and thus by the universal property $u_{ij}\mapsto \sum_{k=1}^Nu_{ik}\otimes u_{kj}$ is a *-homomorphism… the comultiplication giving $C(S_N^+)$ the structure of a compact quantum group.

Commutative Examples

If a universal $\mathrm{C}^*$ algebra is commutative (as in commutativity, $[g_i,g_j]=0$ , is one of the relations, vs the relations imply commutativity, as in $C(S_3^+)$ (nice exercise)), we write $\mathrm{C}^*_{\text{comm}}(\mathrm{G}\mid \mathrm{R})$ . In this case Gelfand’s Theorem, that $\mathrm{C}^*_{\text{comm}}(\mathrm{G}\mid \mathrm{R})\cong C(\text{characters})$ , often allows us to easily identity the algebra (vs the noncommutative case where the universal algebra is mostly studied via models, quotients).

Theorem

If $A$ is a (polynomial) universal commutative $\mathrm{C}^*$ -algebra, then it of the form $C(X)$ , and $X$ is given by the tuples $(z_1,\dots,z_n)\subset\mathbb{C}^n$ that satisfy the relations of of $A$ .

Proof: Characters are *-homomorphisms $A\to \mathbb{C}$ .

Suppose that $z_1,\dots,z_n$ satisfy the relations. Then by the universal property, $\varphi(g_i)=z_i$ is a *-homomorphism.

On the contrary, suppose that $\varphi$ is a character. Then the relations are preserved under a *-homomorphism.

Examples

For $A_0:=\mathrm{C}_{\text{comm}}^*(p,q,1\mid p\text{ and }q\text{ are projections})$ , projections in $\mathbb{C}$ are just the scalars zero and one. Thus the spectrum is $\{(0,0),(1,0),(0,1),(1,1)\}$ and $A_0$ is the algebra of continuous functions on four points.

For $\mathrm{C}_{\text{comm}}^*\left(u_{ij}\mid u\text{ an }N\times N\text{ magic unitary}\right)$ collect the tuple of $N^2$ generators in a matrix. The relations imply that each such tuple is in fact a permutation matrix, and so the universal algebra above is the algebra of continuous functions on $S_N$ .

For

$\displaystyle \mathrm{C}_{\text{comm}}^*\left(g_1,\dots,g_n\mid g_i=g_i^*,\,\sum_i g_i^2=1\right)$

you end up with tuples of $n$ real numbers in $[-1,1]$ whose sum of squares is one… otherwise known as the sphere $\mathcal{S}^{n-1}$ .

Liberations

An interesting business here is to start with a universal commutative $\mathrm{C}^*$ algebra, say one of the three examples above… and see do you get something strictly bigger, necessarily non-commutative, if you drop commutativity. In the above, yes you do. Gelfand’s theorem says that a commutative unital $\mathrm{C}^*$ -algebra is the algebra of continuous functions on a compact space $X$ (which we call a classical space). The Gelfand Philosophy says therefore that a noncommutative unital $\mathrm{C}^*$ -algebra $A$ can be thought of as the algebra of continuous functions on a compact quantum space $\mathbb{X}$ . Note here $\mathbb{X}$ is not a set-of-points, but a virtual object, and strictly $A=C(\mathbb{X})$ is just notation (but see here).

Liberating the second example above from commutativity is the passage from the permutation group $S_N$ to the quantum permutation group $S_N^+$ . Liberating the third example above gives the passage from the real sphere $\mathcal{S}^{n-1}$ to a quantum sphere called the free sphere $\mathcal{S}^{n-1}_+$ .

We can also, of course, work in the other direction, imposing commutativity on not-necessarily universal $\mathrm{C}^*(\mathcal{G}\mid\mathcal{R})$ . If we write $\mathrm{C}^*(\mathcal{G}\mid\mathcal{R})=C(\mathbb{X})$ , then imposing commutativity gives us the classical version $X$ of $\mathbb{X}$ .

Imposing commutativity is not so scary: using the above you just get $\mathrm{C}^*(\mathcal{G}\mid\mathcal{R})\to C(\text{characters})$ … and everything we said above about identifying characters on $\mathrm{C}_{\text{comm}}^*(\mathcal{G}\mid\mathcal{R})$ holds for $\mathrm{C}^*(\mathcal{G}\mid\mathcal{R})$ too.

This can be used: for example if a quantum group acts on a structure $S$ , then its classical version acts on $S$ . This idea was used by Banica and I to show that not every quantum permutation group is the quantum automorphism group of a finite graph (link to *.pdf).

If you have positive elements $f_i$ in a $\mathrm{C}^*$ -algebra with bounded sum, say $\|\sum_i f_i\|\leq C$ then we can bound the summands $\|f_i\|\leq C$ . Write $\sum_if_i=f$ . Note $f$ is positive with norm $C$ . Let $\varphi$ be a state such that $\varphi(f_j)=\|f_j\|$ and apply this to $f$ , $\varphi(\sum_i f_i)=\varphi(f)$ which yields, with $\varphi$ bounded of norm one, $\varphi(f_j)+\sum_{i\neq j}\varphi(f_i)\leq C$ . The result follows by positivity of the sum and the state. To apply to the above play with the $\mathrm{C}^*$ identity. Incidentally, I cannot remember how Murphy proves the existence of $\varphi$ but I like for positive $f$ in a $\mathrm{C}^*$ -algebra, $\mathrm{C}^*(f)\cong C(\sigma(f))$ . Then let $x:=\max_{\lambda\in\sigma(f)}\lambda$ and define a state $\mathrm{ev}_x$ on $\mathrm{C}^*(f)\cong C(\sigma(f))$ . It is the case that $\mathrm{ev}_x(f)=f(x)=\|f\|_{C(\sigma(f))}=x$ , also equal to the norm of $f$ in the ambient algebra (by a spectral radius theorem). Extend the evaluation functional to the whole algebra by Hahn-Banach. ↩︎

Measuring a continuous observable

November 27, 2023 in C*-Algebras & Operator Theory, Research | Leave a comment

I am or rather was interested in the following problem: while we cannot hope to measure with infinite precision in the real world, in the mathematical world can I measure a continuous-spectrum self-adjoint operator given a fixed state? That is measure it with infinite precision?

Let $A=:C(\mathbb{X})$ be a unital $\mathrm{C}^*$ -algebra, and $\varphi\in\mathcal{S}(C(\mathbb{X}))$ a state on it… actually I will use the Gelfand–Birkhoff picture:

$\varphi\in \mathbb{X} \iff \varphi\in\mathcal{S}(C(\mathbb{X}))$

Note that $\varphi$ has an extension to a $\sigma$ -weakly continuous state $\omega_\varphi$ on the bidual, $C(\mathbb{X})^{**}$ . The algebra $C(\mathbb{X})$ sits isometrically in the bidual: the bidual as a von Neumann algebra contains the spectral projections of any self-adjoint $f\in C(\mathbb{X})$ . We use the notation $\mathbf{1}_E(f)$ for Borel $E\subseteq\sigma(f)$ .

Let $\varepsilon> 0$ . Define:

$p_\varepsilon(f)=\mathbf{1}_{(\lambda-\varepsilon,\lambda+\varepsilon)}(f)$ .

Suppose for a state $\varphi\in\mathbb{X}$ that for all $\varepsilon>0$ :

$\omega_\varphi(p_\varepsilon(f))>0$ .

(the situation where $\omega_\varphi(p_\varepsilon(f))=0$ will be moot).

Then we want to consider the entity:

$\displaystyle \varphi_\lambda(g)=\lim_{\varepsilon\to0^+}\frac{\omega_\varphi(p_\varepsilon(f)gp_\varepsilon(f))}{\omega_\varphi(p_\varepsilon(f)}\qquad (g\in C(\mathbb{X}))$ .

If this limit exists then it is a state.

Alas, this limit does not exist in general. There is a commutative counterexample by Nik Weaver on MO, which we will share here.

Let $A=L^{\infty}([0,1])$ and $f\in A$ given by $f(x)=x$ and $\varphi$ integration against Lesbesgue measure. Let $\lambda=0$ and $p_{\varepsilon}=\mathbf{1}_{[0,\varepsilon)}$ .

Define

$\displaystyle S=\bigcup_{n=0}^{\infty} [10^{-(2n+1)},10^{-2n}]$ ,

and $g=\mathbf{1}_S$ , an element of $L^{\infty}([0,1])$ .

Consider $\varphi_0(g)$ and let $\varepsilon =10^{-2m}$ , with $m\in \mathbb{N}$ . It is possible to show that in this case:

$\displaystyle \frac{\varphi(p_\varepsilon gp_\varepsilon)}{\varphi(p_\varepsilon)}=\frac{90}{99}$ .

However, at $\varepsilon=10^{-(2m+1)}$ , we get $1/99$ . This means that the limit $\varphi_0$ above does not exist.

Now, without proof we could expect that for $A=C([0,1])$ , and the same $f$ and $\varphi$ , we could expect that in fact $\varphi_0$ exists, and $\varphi_0(g)=g(0)$ .

The problem here is that for $L^{\infty}([0,1])$ , functions that disagree on a set of measure zero are identified and in general $g(0)$ does not make sense for $g\in L^\infty([0,1])$ .

The best we can do is measure $f\in C(\mathbb{X})$ up to tolerance $\varepsilon>0$ . Say we measure $f\in(\lambda-\varepsilon,\lambda+\varepsilon)$ with a state $\varphi\in \mathbb{X}$ . Then we get conditioning of $\varphi$ to a state:

$\displaystyle \varphi_{\lambda,\varepsilon}(g)=\frac{\varphi(p_{\varepsilon}gp_{\varepsilon})}{\varphi(p_{\varepsilon})}\qquad (g\in C(\mathbb{X}))$

In the commutative case, this is giving the average of $g$ on the interval $(\lambda-\varepsilon,\lambda+\varepsilon)$ .

I had hoped to use $\varphi_\lambda$ to explain why classical spheres don’t admit quantum symmetry. Alas the above means my argument probably cannot work (well, maybe I can use the $\varepsilon$ of room?)

Perhaps we could try and understand in which $\mathrm{C}^*$ -algebras the state $\varphi_\lambda$ is well-defined… but we can say at least for today that we cannot measure continuous observables with infinite precision… even mathematically.

Removing characters with strong relations

November 18, 2023 in C*-Algebras & Operator Theory, Quantum Groups, Research | Leave a comment

…and why it doesn’t work for a quantum alternating group

Despite problems around its existence being well-known, the Google search “quantum alternating group” only gets one (relevant) hit. This is to a paper of Freslon, Teyssier, and Wang, which states:

We therefore have to resort to another idea, which is to compare the process with the so-called pure quantum transposition random walk and prove that they asymptotically coincide. This is a specifically quantum phenomenon connected to the fact that the pure quantum transposition walk has no periodicity issue because there is no quantum alternating group.

Let us explain this a little. Take a deck of $N$ cards, say in some known order. What we are going to do is take two (different) cards at random, and swap them. The question is, does this mix up the deck of cards? What does this question mean? Let $\xi_k\in S_{N}$ be the order of the cards after $k$ of these pure random transposition shuffles. If the shuffles mix up the cards then:

$\displaystyle \lim_{k\to\infty}\mathbb{P}[\xi_k=\sigma]=\frac{1}{N!}\qquad(\sigma\in S_{N})$ .

The random variable $\xi_k$ is a product of $k$ transpositions and using the sign group homomorphism:

$\mathrm{sgn}(\xi_k)=(-1)^k$ .

Take a permutation $\sigma\in S_N$ of odd sign, then:

$\displaystyle \lim_{k\to\infty}\mathbb{P}[\xi_{2k}=\sigma]=0,$

and so this pure random transposition shuffle cannot mix up the deck of cards. The order of the deck alternates (geddit) between $\xi_{2k}\in A_N$ , the alternating group, and $\xi_{2k+1}\in A_N^c$ , the complement of $A_N$ in $S_N$ (if we allow the two cards to be chosen independently, so that there is a chance we pick the same card twice, and do a do-nothing shuffle, then this barrier disappears and this random transposition shuffle does mix up the cards. See Diaconis & Shahshahani).

Amaury Freslon instigated a study of a quantum version of the above random walk. The probability distribution of the shuffles above is:

$\displaystyle \nu=\frac{1}{N}\delta_e+\frac{N-1}{N}\mu_{\text{tr}}$ .

The measure $\mu_{\text{tr}}$ is the measure uniform on transpositions in $S_{N}$ . No such measure makes direct sense in the quantum setting, but if we recast this measure as the measure constant on permutations with $N-2$ fixed points there is a direct analogue, $\varphi_{N-2}$ (see Section 4 for details).

If $u\in M_N(C(S_N^+))$ is the fundamental representation, and $u^c=[\mathbf{1}_{j\to i}]_{i,n=1,...,N}$ , an element of $M_N(C(S_N))$ , the entry-wise abelianisation, the trace $\mathrm{tr}(u^c)\in C(S_N)$ counts the number of fixed points. The functions $\mathbf{1}_{j\to i}$ asking of a permutation, do you map $j\to i$ ? One for yes, zero for no:

$\displaystyle \mathrm{tr}(u^c)(\sigma)=\sum_{k=1}^N\mathbf{1}_{k\to k}(\sigma)=\text{ number of fixed points in }\sigma$ .

Freslon’s $\varphi_{N-2}$ can be thought of as the measure uniform on those quantum permutations that satisfy $\mathrm{tr}(u)=N-2$ .

If you shuffle according to classical $\mu_{\text{tr}}$ , you meet the periodicity issue associated with $\mathrm{sgn}$ . However, there is no such periodicity issue in the quantum case, because there is nothing analogous to a quantum sign homomorphism:

$\mathrm{sgn}^+:S_N^+\to\{-1,1\}$ .

The classical alternating group is:

$\displaystyle A_N=\{\sigma\in S_N\,\colon\,\mathrm{sgn}(\sigma)=1\}$ ,

but with no quantum sign, we don’t seem to be able to define a quantum alternating group in the same way.

This is related to difficulties around the determinant (equal to the sign for permutation matrices). I think, but would have to check, that we can quotient $C(S_N)$ by the relation $\mathrm{det}(u^c)=1$ , and you get $C(A_N)$ in that case… but problems with the determinant mean this cannot happen in the quantum case.

Private communication has shown me a proof that if you quotient any compact matrix quantum group with $\mathrm{det}(u)=1$ , then you get a commutative algebra, that is, a classical group. In particular,

$\displaystyle C(S_N^+)/(\mathrm{det}(u)=1)=C(A_N)$ ,

and not something non-commutative, corresponding to a quantum alternating group $C(A_N^+)$ .

Another way?

This no-go result, which is cool but unpublished, doesn’t rule out a quantum alternating group of the form:

$\displaystyle A_N\subsetneq A_N^+\subsetneq S_N^+$ .

There is indeed for every $N$ a genuine quantum group $\mathbb{G}_N$ with $A_N\subsetneq \mathbb{G}_N$ , but this quantum group does not sit nicely as a quantum subgroup of $S_N^+$ (from here, Section 4).

Given a quantum permutation group $\mathbb{G}\subset S_N^+$ , the set of characters on universal $C(\mathbb{G})$ forms a group $G$ , the classical version of $\mathbb{G}$ . The group law is convolution:

$\displaystyle \varphi_1\star\varphi_2=(\varphi_1\otimes\varphi_2)\Delta$ .

I have a particular interest in characters, and have a pre-print (Section 4) doing some analysis on them. Let $\varphi:C(\mathbb{G})\to \mathbb{C}$ be a character. Then, applying what I call the Birkhoff slice (Section 4.1), $\Phi:\mathcal{S}(C(\mathbb{G}))\to M_N(\mathbb{C})$ , applying a state to the fundamental magic representation component-wise, gives a permutation matrix:

$\displaystyle \Phi(\varphi)=P_\sigma\qquad (\sigma\in S_N)$ .

In this case we write $\varphi=\mathrm{ev}_\sigma$ , and where $\pi_{\text{ab}}$ is the abelianisation, $u_{ij}\mapsto \mathbf{1}_{j\to i}$ :

$\displaystyle \mathrm{ev}_\sigma(f)=\pi_{\text{ab}}(f)(\sigma)\qquad (f\in C(\mathbb{G}))$ .

The characters have support projections, and these in general do not live in $C(\mathbb{G})$ but in the bidual $C(\mathbb{G})^{**}$ . These support projections live in the strong closure of $C(\mathbb{G})$ in its bidual. Briefly, let:

$f_\sigma=u_{\sigma(1),1}u_{\sigma(2),2}\cdots u_{\sigma(N),N}$ .

(as an aside, if we transpose in $f_{\sigma}$ the indices, so $u_{k,\sigma(k)}$ instead of $u_{\sigma(k),k}$ , then $\mathrm{det}(u)=\sum_{\sigma\in S_N}\mathrm{sgn}(\sigma)f_\sigma$ .)

It turns out that the support projection $p_\sigma$ of $\mathrm{ev}_\sigma$ is the strong limit of $(f_\sigma^n)_{n\geq 1}$ … and if $(f_\tau^n)_{n\geq 1}$ converges to zero… then $\mathrm{ev}_{\tau}$ is zero, not a character, and $\tau$ is not in the classical version of $\mathbb{G}$ .

Enter this talk by Gilles Gonçalves De Castro (Universidade Federal de Santa Catarina, Brazil), who teaches us with his coauthor Giulioano Boava that it is possible to include (admissible) strong as well as norm relations in defining a universal $\mathrm{C}^*$ -algebra.

An idea!

So, why not take $S_N^+$ , or rather $C(S_N^+)$ , and quotient out the characters in the complement of $A_N$ in $S_N$ ? We can do this via the relations $p_\tau=0$ for $\tau\in A_N^c$ , they are admissible. So… define the following algebra:

$\displaystyle C(A_N^+)=C(S_N^+)/\langle p_\tau=0,\,\tau\in A_N^c\rangle$

There is a lot of work to do here to prove that this is a quantum group… have we a *-homomorphism $\Delta(u_{ij})=\sum_{k=1}^N u_{ik}\otimes u_{kj}$ ? But at least we have a candidate algebra.

Failure

Actually we don’t. In fact, either the algebra does not admit a quantum group structure OR

$C(A_N^+)=C(S_N^+)$ ,

Unfortunately, because of non-coamenability issues, lots of algebras of continuous functions on quantum permutation groups also have $p_\sigma=0$ for all $\sigma\in S_{N}$ … not because they have no classical versions, but because classical versions are defined on the universal level… where there are always characters… at the reduced level the algebras admit no characters.

In particular, the reduced algebra of functions $C_{\text{r}}(S_N^+)$ satisfies $p_\sigma=0$ for all $\sigma\in S_N$ , and so, if we assume that $C(A_N^+)$ DOES have a quantum group structure, we have a comultiplication preserving quotient:

$C(A_N^+)\to C_{\text{r}}(S_N^+)$ .

Then with the help of J. De Ro, this means we have a Hopf*-algebra morphism on the level of the dense Hopf*-algebras, saying that $S_N^+$ is a quantum subgroup of $A_N^+$ . But of course this $A_N^+$ is a quantum subgroup of $S_N^+$ and so it follows in this case that the two quantum groups coincide.

This isn’t a great no-go theorem: but a log of something that doesn’t work. And of course this approach doesn’t work for any subgroup of $S_N$ .

A probability question on card shuffling

November 17, 2023 in General, Probability Theory | Leave a comment

Alice, Bob and Carol are hanging around, messing with playing cards.

Alice and Bob each have a new deck of cards, and Alice, Bob, and Carol all know what order the decks are in.

Carol has to go away for a few hours.

Alice starts shuffling the deck of cards with the following weird shuffle: she selects two (different) cards at random, and swaps them. She does this for hours, doing it hundreds and hundreds of times.

Bob does the same with his deck.

Carol comes back and asked “have you mixed up those decks yet?” A deck of cards is “mixed up” if each possible order is approximately equally likely:

$\displaystyle \mathbb{P}[\text{ deck in order }\sigma\in S_{52}]\approx \frac{1}{52!}$

She asks Alice how many times she shuffled the deck. Alice says she doesn’t know, but it was hundreds, nay thousands of times. Carol says, great, your deck is mixed up!

Bob pipes up and says “I don’t know how many times I shuffled either. But I am fairly sure it was over a thousand”. Carol was just about to say, great job mixing up the deck, when Bob interjects “I do know that I did an even number of shuffles though.“.

Why does this mean that Bob’s deck isn’t mixed up?

Talk about idempotent states

June 1, 2023 in Quantum Groups, Random Walks on Finite Quantum Groups, Research, Research Updates | Leave a comment

I gave a talk to the Quantum Groups & Interactions Workshop in Glasgow.

Abstract: Woronowicz proved the existence of the Haar state for compact quantum groups under a separability assumption later removed by Van Daele in a new existence proof. A minor adaptation of Van Daele’s proof yields an idempotent state in any non-empty weak*-compact convolution-closed convex subset of the state space. Such subsets, and their associated idempotent states, are studied in the case of quantum permutation groups.

glasgowv5 Download

Talks about the Frucht property

June 1, 2023 in C*-Algebras & Operator Theory, Quantum Groups, Research, Research Updates | Leave a comment

I gave the same talk to the Non local games seminar and C*-Days in Prague:

Abstract: The first part of the talk will give a post hoc motivation for Banica’s 2005 definition of the quantum automorphism group of a finite graph, and in doing so attempt to build a good intuition for quantum automorphism. Frucht in 1939 showed that every finite group is the automorphism group of a finite graph, and a natural pursuit in the theory of quantum automorphism groups is to establish quantum analogues of this result. Based on a joint work with Banica, the second part of the talk will address this question.

Slides below, video here from the Prague NCGT Group’s YouTube:

The slides are subtly different: the one for C*-Days is the latest version:

praguev5 Download

	J.P. McCarthy on MATH6040: Spring 2022, Week…
	J.P. McCarthy on MATH6040: Spring 2022, Week…
	J.P. McCarthy on MATH7019: Winter 2020, Week…
	J.P. McCarthy on MATH7019: Winter 2020, Week…
	A Sufficient Conditi… on Almost All Trees have Quantum…

Category Archive

An approach to the maximality conjecture for quantum permutation groups

Definition 1 (Commutator and Isotropy Ideals)

Lemma 1

Proposition 1

Theorem 1 (Wang/Banica/Bichon)

On the number of fixed points of conditioned quantum permutations

Theorem

Local vs Global Conditioning of Quantum Permutations

Epilogue?

A strange property of quantum permutations

Classical Warm-up

Let’s Go Quantum

A twist

An interesting addend to Tracing the orbitals of the quantum permutation group

A note on universal C*-algebras

Idea and Intuition

Two Examples

Commutative Examples

Theorem

Examples

Liberations

Measuring a continuous observable

Removing characters with strong relations

…and why it doesn’t work for a quantum alternating group

Another way?

An idea!

Failure

A probability question on card shuffling

Talk about idempotent states

Talks about the Frucht property

Recent Comments

Categories

J.P. McCarthy Maths

Category Archive

Definition 1 (Commutator and Isotropy Ideals)

Lemma 1

Proposition 1

Theorem 1 (Wang/Banica/Bichon)

Share this:

Theorem

Local vs Global Conditioning of Quantum Permutations

Epilogue?

Share this:

Classical Warm-up

Let’s Go Quantum

A twist

Share this:

Share this:

Idea and Intuition

Two Examples

Commutative Examples

Theorem

Examples

Liberations

Share this:

Share this:

…and why it doesn’t work for a quantum alternating group

Another way?

An idea!

Failure

Share this:

Share this:

Share this:

Share this:

Recent Comments

Categories