Category Archive

You are currently browsing the category archive for the ‘Random Walks on Finite Quantum Groups’ category.

Talk about idempotent states

June 1, 2023 in Quantum Groups, Random Walks on Finite Quantum Groups, Research, Research Updates | Leave a comment

I gave a talk to the Quantum Groups & Interactions Workshop in Glasgow.

Abstract: Woronowicz proved the existence of the Haar state for compact quantum groups under a separability assumption later removed by Van Daele in a new existence proof. A minor adaptation of Van Daele’s proof yields an idempotent state in any non-empty weak*-compact convolution-closed convex subset of the state space. Such subsets, and their associated idempotent states, are studied in the case of quantum permutation groups.

glasgowv5 Download

Talk: The Kawada-Ito theorem for quantum groups

October 10, 2022 in C*-Algebras & Operator Theory, Quantum Groups, Random Walks on Finite Quantum Groups, Research, Research Updates | Leave a comment

BCRI Mini-Symposium: Noncommutative Probability & Quantum Information

Monday, 10^th October 2022 from 12:00 to 15:00

Organizers: Claus Koestler (UCC), Stephen Wills (UCC)

SPEAKER: J.P. McCarthy (Munster Technological University)
TITLE: The Kawada-Itô theorem for finite quantum groups.
ABSTRACT: Necessary and sufficient conditions for a Markov chain to be ergodic are that the chain is irreducible and aperiodic. This result is manifest in the case of random walks on finite groups by a statement about the support of the driving probability: a random walk on a finite group is ergodic if and only if the support is not concentrated on a proper subgroup, nor on a coset of a proper normal subgroup. The study of random walks on finite groups extends naturally to the study of random walks on compact quantum groups, where a state on the algebra of functions plays the role of the driving probability. A random walk on a compact quantum group can fail to be irreducible without being concentrated on a proper quantum subgroup. In this talk we will explore this phenomenon. Time allowing, we will talk about periodicity, and as a conclusion, I give necessary and sufficient conditions for ergodicity of a random walk on a finite quantum group in terms of the support projection of the driving state.

In the end the talk (below) didn’t quite match the abstract.

kitv1 Download

The Ergodic Theorem for Random Walks on Finite Quantum Groups

April 2, 2020 in C*-Algebras & Operator Theory, Probability Theory, Quantum Groups, Random Walks on Finite Quantum Groups, Research, Research Updates | 1 comment

Abstract

Necessary and sufficient conditions for a Markov chain to be ergodic are that the chain is irreducible and aperiodic. This result is manifest in the case of random walks on finite groups by a statement about the support of the driving probability: a random walk on a finite group is ergodic if and only if the support is not concentrated on a proper subgroup, nor on a coset of a proper normal subgroup. The study of random walks on finite groups extends naturally to the study of random walks on finite quantum groups, where a state on the algebra of functions plays the role of the driving probability. Necessary and sufficient conditions for ergodicity of a random walk on a finite quantum group are given on the support projection of the driving state.

Link to journal here.

Freslon’s Ergodic Theorem for (Finite) Group Algebras

December 17, 2019 in Quantum Groups, Random Walks on Finite Quantum Groups, Research | Leave a comment

In the hope of gleaning information for the study of aperiodic random walks on (finite) quantum groups, which I am struggling with here, by couching Freslon’s Proposition 3.2, in the language of Fagnola and Pellicer, and in the language of my (failed) attempts (see here, here, and here) to find the necessary and sufficient conditions for a random walk to be aperiodic. It will be necessary to extract the irreducibility and aperiodicity from Freslon’s rather ‘unilateral’ result.

Well… I have an inkling that because dual groups satisfy what I would call the condition of abelianness (under the ‘quantisation’ functor), all (quantum) subgroups are normal… this is probably an obvious thing to write down (although I must search the literature) to ensure it is indeed known (or is untrue?). Edit: Wang had it already, see the last proposition here.

Let $F(G)$ be a the algebra of functions on a finite classical (as opposed to quantum) group $G$ . This has the structure of both an algebra and a coalgebra, with an appropriate relationship between these two structures. By taking the dual, we get the group algebra, $\mathbb{C}G=:F(\widehat{G})$ . The dual of the pointwise-multiplication in $F(G)$ is a coproduct for the algebra of functions on the dual group $\widehat{G}$ … this is all well known stuff.

Recall that the set of probabilities on a finite quantum group is the set of states $M_p(G):=\mathcal{S}(F(G))$ , and this lives in the dual, and the dual of $F(\widehat{G})$ is $F(G)$ , and so probabilities on $\widehat{G}$ are functions on $G$ . To be positive is to be positive definite, and to be normalised to one is to have $u(\delta^e)=1$ .

The ‘simplicity’ of the coproduct,

$\Delta(\delta^g)=\delta^g\otimes\delta^g$ ,

means that for $u\in M_p(\widehat{G})$ ,

$(u\star u)(\delta^g)=(u\otimes u)\Delta(\delta^g)=u(\delta^g)^2$ ,

so that, inductively, $u^{\star k}$ is equal to the (pointwise-multiplication power) $u^k$ .

The Haar state on $\widehat{G}$ is equal to:

$\displaystyle \pi:=\int_{\hat{G}}:=\delta_e$ ,

and therefore necessary and sufficient conditions for the convergence of $u^{\star k}\rightarrow \pi$ is that $u$ is strict. It can be shown that for any $u\in M_p(G)$ that $|u(\delta^g)|\leq u(\delta^e)=1$ . Strictness is that this is a strict inequality for $g\neq e$ , in which case it is obvious that $u^{\star k}\rightarrow \delta_e$ .

Here is a finite version of Freslon’s result which holds for discrete groups.

Freslon’s Ergodic Theorem for (Finite) Group Algebras

Let $u\in M_p(\widehat{G})$ be a probability on the dual of finite group. The random walk generated by $u$ is ergodic if and only if $u$ is not-concentrated on a character on a non-trivial subgroup $H\subset G$ .

Freslon’s proof passes through the following equivalent condition:

The random walk on $\widehat{G}$ driven by $u\in M_p(\widehat{G})$ is not ergodic if $u$ is bimodularwith respect to a non-trivial subgroup $H\subset G$ , in the sense that

$\displaystyle u(\underbrace{\delta^g\delta^h}_{=\delta^{gh}})=u(\delta^g)u(\delta^h)=u\left(\underbrace{\delta^h\delta^g}_{=\delta^{hg}}\right)$ .

Before looking at the proof proper, we might note what happens when $G$ is abelian, in which case $\widehat{G}$ is a classical group, the set of characters on $G$ .

To every positive definite function $u\in M_p(\widehat{G})$ , we can associate a probability $\nu_u\in M_p(\widehat{G})$ such that:

$\displaystyle u(\delta^g)=\sum_{\chi\in\hat{G}} \chi(\delta^g) \nu_u(\chi)$ .

This is Bochner’s Theorem for finite abelian groups. This implies that positive definite functions on finite abelian groups are exactly convex combinations of characters.

Freslon’s condition says that to be not ergodic, $u$ must be a character on a non-trivial subgroup $H\subset G$ . Such characters can be extended in $[G\,:\,H]$ ways.

Therefore, if $u$ is not ergodic, $u_{\left|H\right.}=\eta\in \widehat{H}$ .

For $h\in H$ , we have

$\displaystyle u(h)=\sum_{\chi\in\widehat{G}}\chi(h)\nu_u(\chi)$ ,

dividing both sides by $u(h)=\eta(h)\neq 0$ yields:

$\displaystyle\sum_{\chi \in \widehat{G}} (\eta^{-1}\chi)(h)\nu_u (\chi)=1$ .

As $\nu_u\in M_p(\widehat{G})$ , and $(\eta^{-1}\chi)(h)\in \mathbb{T}$ , this implies that $\nu_u$ is supported on characters such that, for all $h\in H$ :

$\eta^{-1}(h)\chi(h)=1\Rightarrow \chi=\eta\tilde{\chi}$ ,

such that $\tilde{\chi}(H)=\{1\}$ . The set of such $\tilde{\chi}$ is the annihilator of $H$ in $\widehat{G}$ , and it is a subgroup. Therefore $\nu_u$ is concentrated on the coset of a normal subgroup (as all subgroups of an abelian group are normal).

This, via Pontragin duality, is not looking at the ‘support’ of $u$ , but rather of $\nu_u$ . Although we denote $\mathbb{C}G=:F(\widehat{G})$ , and when $G$ is abelian, $\widehat{G}$ is a group (unnaturally, of characters) isomorphic to $G$ . Is it the case though that,

$\Delta(\chi)=\chi\otimes\chi$

gives the same object in as

$\displaystyle\Delta(\chi)=\sum_{g\in G}\chi(\delta^g)\Delta(\delta_g)$

$\displaystyle =\sum_{g\in G}\chi(\delta^g)\sum_{t\in G}\delta_{gt^{-1}}\otimes \delta_t$ ?

Well… of course this is true because $\chi(gh)=\chi(g)\chi(h)$ .

We could proceed to look at Fagnola & Pellicer’s work but first let us prove Freslon’s result, hopefully in the finite case the analysis disappears…

Proof: Assume that $u$ is not strict and let

$\Lambda:=|u|^{-1}(\{1\})$ .

There exists a unitary representation $\Phi:G\rightarrow B(H)$ and a unit vector $\xi$ such that

$u(g)=\langle \Phi(g)\xi,\xi\rangle$

Cauchy-Schwarz implies that

$|u(g)|\leq \|\Phi(g)\xi\|\|\xi\|=\|\xi\|^2$ .

If $h$ is not strict there is an $h$ such that this is an inequality and so $\Phi(h)\xi$ is colinear to $\xi$ , it follows that $\Phi(h)\xi=u(h)\xi$ .

This implies for $h\in \Lambda$ and $g\in G$ :

$|u(gh)|=|\langle \Phi(gh)\xi,\xi\rangle|=|u(h)||\langle \Phi(g)\xi,\xi\rangle|=|u(g)|$ ,

and so $\Lambda$ is closed under multiplication. Also $u(g^{-1})=\overline{u(g)}$ and so $\Lambda$ and so $\Lambda$ is a subgroup. It follows that $u$ is a character on $\Lambda$ , which is not trivial because $u$ is not strict.

I don’t really need to go through the third equivalent condition. If $u$ coincides with a character on a subgroup $\Lambda$ , for $h\in \Lambda$

$|u(h)|^2=u(h)\overline{u(h)}=u(h)u(h^{-1})=u(e)=1$ ,

and so $u$ is not strict $\bullet$

Now let us look at the language of Fagnola and Pellicer. What is a projection in $\mathbb{C}G$ ? First note the involution in $\mathbb{C}G$ is $(\delta^g)^*=\delta^{g^{-1}}$ . The second multiplication is the convolution. This means projections in the algebra are symmetric with respect to the group inverses and they are also idempotents. They are actually equal to Haar states on finite subgroups.

I think periodicity is also wrapped up in Freslon’s result as I think all subgroups of dual groups are normal. Perhaps, oddly, not being concentrated on a subgroup means that the positive function (probability on the dual) is one on that subgroup…

Well… let us start with irreducible. Suppose $u$ fails to be ergodic because it is irreducible. This means there is a projection $p_H=\int_H$ such that that $P_u(p_H)=p_H$ (and support $u$ less than $p_H$ ?)

Let us look at the first condition:

$P_u(p_H)=(u\otimes I)\Delta(p_H)=\cdots=\frac{1}{|H|}\sum_{h\in H}u(h)\delta^h=p_H\Rightarrow u_{\left|H\right.}=1$ .

What now is the support of $u$ ? Well… some work I have done offline shows that the special projections, the group-like projections, correspond to to $\pi_H$ for $H$ a subgroup of $G$ . If $u$ is reducible, it is concentrated on such a quasi-subgroup, and this means that $u$ coincides with a trivial character on $H$ . In terms of Fagnola Pellicer, $P_u(\pi_H)=\pi_H$ .

Now let us tackle aperiodicity. It is going to correspond, I think, with being concentrated on a ‘coset’ of a non-trivial character on $H$ …

Well, we can show that if $u$ is periodic, there is a subset $S\subset G$ such that $u(s)=e^{2\pi i a_s/d}$ for all $s\in S$ . We can use Freslon’s proof to show that $S$ is in a subgroup on which $|u|=1$ .

Now what I want to do is put this in the language of ‘inclusion’ matrices… but the inclusions for cocommutative quantum groups are trivial so no go…

We can reduce Freslon’s conditions down to irreducible and aperiodic: not coinciding with a trivial character, and not coinciding with a character.

Periodicity of Random Walks on Finite Quantum Groups

September 12, 2019 in Quantum Groups, Random Walks on Finite Quantum Groups, Research Updates | Leave a comment

In the case of a finite classical group $G$ , we can show that if we have i.i.d. random variables $\zeta_i\sim\nu\in M_p(G)$ , that if $\text{supp }\nu\subset Ng$ , for $Ng$ a coset of a proper normal subgroup $N\rhd G$ , that the random walk on $G$ driven by $\nu$ , the random variables:

$\xi_k=\zeta_k\cdots \zeta_1$ ,

exhibits a periodicity because

$\xi_k\in Ng^{k}$ .

This shows that a necessary condition for ergodicity of a random walk on a finite classical group $G$ driven by $\nu\in M_p(G)$ is that the support of $\nu$ not be concentrated on the coset of a proper normal subgroup.

I had hoped that something similar might hold for the case of random walks on finite quantum groups but alas I think I have found a barrier.

Read the rest of this entry »

The Ergodic Theorem for Random Walks: from Finite Groups, to Group Algebras, to Finite Quantum Groups

September 6, 2019 in Quantum Groups, Random Walks on Finite Quantum Groups, Research | Leave a comment

Slides of a talk given at Munster Groups 2019, WIT.

Abstract: It is a folklore theorem that necessary and sufficient conditions for a random walk on a finite group to converge in distribution to the uniform distribution – “to random” – are that the driving probability is not concentrated on a proper subgroup nor the coset of a proper normal subgroup. This is the Ergodic Theorem for Random Walks on Finite Groups. In this talk we will outline the rarely written down proof, and explain why, for example, adjacent transpositions can never mix up a deck of cards. From here we will, in a very leisurely and natural fashion, introduce (and motivate the definition of) finite quantum groups, and random walks on them. We will see how the group algebra of a finite group is the algebra of functions on a finite quantum group. Freslon has very recently proved the Ergodic Theorem in this setting, and we present ongoing work towards an Ergodic Theorem in the more general finite quantum group setting; a result that would generalise both the folklore and group algebra Ergodic Theorems.

Finite Quantum Groups: Pure States

June 25, 2019 in Quantum Groups, Random Walks on Finite Quantum Groups, Research | Leave a comment

Introduction

Every finite quantum group has finite dimensional algebra of functions:

$\displaystyle F(G)=\bigoplus_{j=1}^m M_{n_j}(\mathbb{C})$ .

At least one of the factors must be one-dimensional to account for the counit $\varepsilon:F(G)\rightarrow \mathbb{C}$ , and if this factor is denoted $\mathbb{C}e_1$ , the counit is given by the dual element $e^1$ . There may be more and so reorder the index $j\mapsto i$ so that $n_i=1$ for $i=1,\dots,m_1$ , and $n_i>1$ for $i>m_1$ :

$\displaystyle F(G)=\left(\bigoplus_{i=1}^{m_1} \mathbb{C}e_{i}\right)\oplus \bigoplus_{i=m_1+1}^m M_{n_i}(\mathbb{C})=:A_1\oplus B$ ,

Denote by $M_p(G)$ the states of $F(G)$ . The pure states of $F(G)$ arise as pure states on single factors.

In the case of the Kac-Paljutkin and Sekine quantum groups, the convolution powers of pure states exhibit a periodicity of sorts. Recall for these quantum groups that $B$ consists of a single matrix factor.

In these cases, for pure states of the form $e^i$ , that is supported on $A_1$ (and we can say a little more than is necessary), the convolution remains supported on $A_1$ because

$\Delta(A_1)\subset A_1\otimes A_1+B\otimes B$ .

If we have a pure state $\nu$ supported on $B=M_{\sqrt{\dim B}}(\mathbb{C})$ , then because

$\Delta(B)\subset A_1\otimes B+B\otimes A_1$ ,

then $\nu\star\nu$ must be supported on, because of $\Delta(A_1)\subset A_1\otimes A_1+B\otimes B$ , $A_1$ .

Inductively all of the $\nu^{\star 2k}$ are supported on $A_1$ and the $\nu^{\star 2k+1}$ are supported on $B$ . This means that the convolutions powers of a pure state, in these cases, cannot converge to the Haar state.

The question is, do the results above about the image of $A_1$ and $B$ under the coproduct hold more generally? I believe that the paper of Kac and Paljutkin shows that this is the case whenever $B$ consists of a single factor… but does it hold more generally?

To find out we go back and do some sandboxing with the paper of Kac and Paljutkin. Which is a pleasure because that paper is beautiful. The blue stuff is my own scribbling.

Finite Ring Groups

Let $G$ be a finite quantum group with notation on the algebra of functions as above. Note that $A_1$ is commutative. Let

$p=\sum_{i=1}^{m_1}e_i$ ,

which is a central idempotent.

Lemma 8.1

$S(p)=p$ .

Proof: If $S(\mathbf{1}_G-p)p\neq 0$ , then for some $i>m_1$ , and $f\in M_{n_i}(\mathbb{C})$ , the mapping $f\mapsto S(f)p$ is a non-zero homomorphism from $M_{n_i}(\mathbb{C})$ into commutative $A_1$ which is impossible.

If $S(\mathbf{1}_G-p)p=g\neq 0$ , then one of the $S(I_{n_i})\in A_1\oplus B$ , with ‘something’ in $A_1$ . Using the centrality and projectionality of $p$ , we can show that the given map is indeed a homomorphism.

It follows that $S(p)p=p\Rightarrow S(S(p)p)=S(p)=S(p)p=S(p)$ , and so $p=S(p)$ $\bullet$

Lemma 8.2

$(p\otimes p)\Delta(p)=p\otimes p$

Proof: Suppose that $(p\otimes p)\Delta(f)=b$ for some non-commutative $f\in M_{n_i}(\mathbb{C})$ . This means that there exists an index $k$ such that $f_{(1)_k}\otimes f_{(2)_k}\in A_1\otimes A_1$ . Then for that factor,

$f\mapsto \Delta(f)(p\otimes p)$

is a non-null homomorphism from the non-commutative into the commutative.

We see that $(p\otimes p)\Delta(f)=0$ for all $f\in B$ . Putting $a=\mathbf{1}-p$ we get the result $\bullet$

The following says that $p$ is a group-like projection. We know from previous work that if a state is supported on a group-like projection that it will remain supported on it. In particular, any state supported on $A_1$ will remain there.

Lemma 8.3

$(p\otimes \mathbf{1}_G)\Delta(p)=p\otimes p=(\mathbf{1}_G\otimes p)\Delta(p)$ .

Proof: Since $\Delta$ is a homomorphism, $\Delta(p)$ is an idempotent in $F(G)\otimes F(G)$ . I do not understand nor require the rest of the proof.

Lemma 8.4

$A_1=F(G_1)$ is the algebra of functions on finite group with elements $i=1,\dots,m_1$ , and we write $e_i=\delta_i$ . The coproduct is given by $(p\otimes p)\Delta$ .

We have:

$(p\otimes p)\Delta(e_i)=\sum_{t\in G_1}\delta_{it^{-1}}\otimes \delta_t$ ,

$S(\delta_i)=\delta_{i^{-1}}$ ,

$\varepsilon(e_i)=\delta_{i,1}$ ,

as $e_1=\delta_e$ .

The element $\Delta(\delta_i)$ is a sum of four terms, lying in the subalgebras:

$A_1\otimes A_1,\,B\otimes B,\,A_1\otimes B,\,B\otimes A_1$ .

We already know what is going on with the first summand. Denote the second by $P_i$ . From the group-like-projection property, the last two summands are zero, so that

$\Delta(\delta_i)=\sum_{t\in G_1}\delta_{t}\otimes \delta_{t^{-1}i}+P_i$ .

Since the $\delta_i$ are symmetric ( $\delta_i^*=\delta_i$ ) mutually orthogonal idempotents, $P_i$ has similar properties:

$P_i^*=P_i,\,P_i^2=P_i,\,P_iP_j=0$

for $i\neq j$ .

At this point Kac and Paljutkin restrict to $B=M_{n_{i+1}}(\mathbb{C})$ , that is there is only one summand. Here we try to keep arbitrarily (finitely) many summands in $B$ .

Let the summand $M_{n_i}(\mathbb{C})$ have matrix units $E_{mn}^i$ , where $m,n=1,\dots,n_i$ . Kac and Paljutkin now do something which I think is a little dodgy, but basically that the integral over $G$ is equal on each of the $\delta_i$ , equal on each of the $E_{mm}^i$ , and then zero off the diagonal.

It does follow from above that each $P_i\in B\otimes B$ is a projection.

Now I am stuck!

Periodicity & Aperiodicity for Random Walks on Quantum Groups

June 7, 2019 in Quantum Groups, Random Walks on Finite Quantum Groups, Research | Leave a comment

Background

I am trying to prove an Ergodic Theorem for Random Walks on Finite Quantum Groups. A random walk on a quantum group driven by $\nu\in M_p(G)$ is ergodic if the convolution powers $(\nu^{\star k})_{k\geq 0}$ converge to the Haar state $\int_G$ .

The classical theorem for finite groups:

Ergodic Theorem for Random Walks on Finite Groups

A random walk on a finite group $G$ driven by a probability $\nu\in M_p(G)$ is ergodic if and only if $\nu$ is not concentrated on a proper subgroup nor the coset of a proper normal subgroup.

Not concentrated on a proper subgroup gives irreducibility. A random walk is irreducible if for all $g\in G$ , there exists $k\in\mathbb{N}$ such that $\nu^{\star k}(\{g\})>0$ .

Not concentrated on the coset of a proper normal subgroup gives aperiodicity. Something which should be equivalent to aperiodicity is if

$p:=\gcd\{k>0:\nu^{\star k}(e)>0\}$

is equal to one (perhaps via invariance $\mathbb{P}[\xi_{i+1}=t|\xi_{i}=s]=\mathbb{P}[\xi_{i+1}=th|\xi_{i}=sh]$ ).

If $\nu$ is concentrated on the coset a proper normal subgroup $N\rhd G$ , specifically on $Ng\neq Ne$ , then we have periodicity ( $Ng\rightarrow Ng^2\rightarrow \cdots\rightarrow Ng^{o(g)}=Ne\rightarrow Ng\rightarrow \cdots$ ), and $p=o(g)$ , the order of $g$ .

In Markov chain theory, ergodicity is equivalent to irreduciblity and aperiodicity.

The theorem in the quantum case should look like:

Ergodic Theorem for Random Walks on Finite Quantum Groups

A random walk on a finite quantum group $G$ driven by a state $\nu\in M_p(G)$ is ergodic if and only if “X”.

Irreducibility

At the moment I have some part of X;the irreducibility bit. As is well known since Pal (1996), it is possible to have a probability not concentrated on a quantum subgroup be reducible. This led Franz & Skalski to generalise quantum subgroups to group-like-projections, which I will say correspond to quasi-subgroups following Kasprzak & Sołtan.

I have shown that if $\nu$ is concentrated on a proper quasi-subgroup $S$ , in the sense that $\nu(P_S)=1$ for a group-like-projection $P_S$ , that so are the $\nu^{\star k}$ . The analogue of irreducible is that for all $q$ projections in $F(G)$ , there exists $k\in\mathbb{N}$ such that $\nu^{\star k}(q)>0$ . If $\nu$ is concentrated on a quasi-subgroup $S$ , then for all $k$ , $\nu^{\star k}(Q_S)=0$ , where $Q_S=\mathbf{1}_G -P_S$ .

I have also shown on the other hand that if the random walk is reducible that it must be concentrated on a proper quasi-subgroup. Franz & Skalski show that group-like-projections also have a correspondence with idempotent states. The Césaro Means

$\displaystyle \nu_n:=\frac{1}{n}\sum_{k=1}^n\nu^{\star k}$ ,

converge to an idempotent state $\nu_\infty$ . If $\nu^{\star k}(q)=0$ for all $k$ then the $\nu_{\infty}(q)=0$ also, so that $\nu_\infty\neq \int_G$ (as the Haar state is faithful). I was able to prove that $\nu$ is supported on the quasi-subgroup given by the idempotent $\nu_\infty$ .

I believe this result — irreducible if and only if not concentrated on a quasi-subgroup — holds more generally than just in finite quantum groups.

Read the rest of this entry »

Some Unresolved and Unexplored Aspects of Random Walks on Quantum Groups

May 14, 2019 in Quantum Groups, Random Walks on Finite Quantum Groups, Research | 1 comment

Slides of a talk given to the Functional Analysis seminar in Besancon.

Some of these problems have since been solved.

“e in support” implies convergence

Consider a $\nu\in M_p(G)$ on a finite quantum group such that where

$M_p(G)\subset \mathbb{C}\varepsilon \oplus (\ker \varepsilon)^*$ ,

$\nu=\nu(e)\varepsilon+\psi$ with $\nu(e)>0$ . This has a positive density of trace one (with respect to the Haar state $\int_G\in M_p(G)$ ), say

$\displaystyle a_\nu=\nu(e)\eta+b_\psi\in \mathbb{C}\eta\oplus \ker \varepsilon$ ,

where $\eta$ is the Haar element.

An element in a direct sum is positive if and only if both elements are positive. The Haar element is positive and so $b_\psi\geq 0$ . Assume that $b_\psi\neq 0$ (if $b_\psi=0$ , then $\psi=0\Rightarrow \nu=\varepsilon\Rightarrow \nu^{\star k}=\varepsilon$ for all $k$ and we have trivial convergence)

Therefore let

$\displaystyle a_{\tilde{\psi}}:=\frac{b_\psi}{\int_G b_\psi}$

be the density of $\tilde{\psi}\in M_p(G)$ .

Now we can explicitly write

$\displaystyle \nu=\nu(e)\varepsilon+(1-\nu(e))\tilde{\psi}$ .

This has stochastic operator

$P_\nu=\nu(e)I_{F(G)}+(1-\nu(e))P_{\tilde{\psi}}$ .

Let $\lambda$ be an eigenvalue of $P_\nu$ of eigenvector $a$ . This yields

$\nu(e)a+(1-\nu(e))P_{\tilde{\psi}}(a)=\lambda a$

and thus

$\displaystyle P_{\tilde{\psi}}a=\frac{\lambda-\nu(e)}{1-\nu(e)}a$ .

Therefore, as $a$ is also an eigenvector for $P_{\tilde{\psi}}$ , and $P_{\tilde{\psi}}$ is a stochastic operator (if $a$ is an eigenvector of eigenvalue $|\lambda|>1$ , then $\|P_\nu a\|_1=|\lambda|\|a\|_1\leq \|a\|_1$ , contradiction), we have

$\displaystyle \left|\frac{\lambda-\nu(e)}{1-\nu(e)}\right|\leq 1$

$\Rightarrow |\lambda-\nu(e)|\leq 1-\nu(e)$ .

This means that the eigenvalues of $P_\nu$ lie in the ball $B_{1-\nu(e)}(\nu(e))$ and thus the only eigenvalue of magnitude one is $\lambda=1$ , which has (left)-eigenvector the stationary distribution of $P_\nu$ , say $\nu_\infty$ .

If $\nu$ is symmetric/reversible in the sense that $\nu=\nu\circ S$ , then $P_\nu$ is self-adjoint and has a basis of (left)-eigenvectors $\{\nu_\infty=:u_1,u_2,\dots,u_{|G|}\}\subset \mathbb{C}G$ and we have, if we write $\nu=\sum_{t=1}^{|G|}a_tu_t$ ,

$\displaystyle \nu^{\star k}=\sum_{t=1}^{|G|}a_t\lambda_t^ku_t$ ,

which converges to $a_1\nu_\infty$ (so that $a_1=1$ ).

If $\nu$ is not reversible, it is a standard argument to show that when put in Jordan normal form, that the powers $P_{\nu}^k$ converge and thus so do the $\nu^{\star k}$ $\bullet$

Total Variation Decrasing

Uses Simeng Wang’s $\|a\star_Ab\|_1\leq \|a\|_1\|b\|_1$ . Result holds for compact Kac if the state has a density.

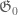
Periodic $e^2$ is concentrated on a coset of a proper normal subgroup of $\mathfrak{G}_0$

$e_2+e_4$ is a minimal projection (coset) in the quotient space of the normal subgroup (to be double checked) given by $\langle e_1,e_3\rangle$

Supported on Subgroup implies Reducible

I have a proof that reducible is equivalent to supported on a pre-subgroup.

Publication

February 25, 2019 in Quantum Groups, Random Walks on Finite Quantum Groups, Research, Research Updates | Leave a comment

Diaconis–Shahshahani Upper Bound Lemma for Finite Quantum Groups, Journal of Fourier Analysis and Applications, doi: 10.1007/s00041-019-09670-4 (earlier preprint available here)

Abstract

A central tool in the study of ergodic random walks on finite groups is the Upper Bound Lemma of Diaconis and Shahshahani. The Upper Bound Lemma uses Fourier analysis on the group to generate upper bounds for the distance to random and thus can be used to determine convergence rates for ergodic walks. The Fourier analysis of quantum groups is remarkably similar to that of classical groups. This allows for a generalisation of the Upper Bound Lemma to an Upper Bound Lemma for finite quantum groups. The Upper Bound Lemma is used to study the convergence of ergodic random walks on the dual group $\widehat{S_n}$ as well as on the truly quantum groups of Sekine.

	J.P. McCarthy on MATH6040: Spring 2022, Week…
	J.P. McCarthy on MATH6040: Spring 2022, Week…
	J.P. McCarthy on MATH7019: Winter 2020, Week…
	J.P. McCarthy on MATH7019: Winter 2020, Week…
	A Sufficient Conditi… on Almost All Trees have Quantum…

Category Archive

Talk about idempotent states

Talk: The Kawada-Ito theorem for quantum groups

The Ergodic Theorem for Random Walks on Finite Quantum Groups

Abstract

Freslon’s Ergodic Theorem for (Finite) Group Algebras

Freslon’s Ergodic Theorem for (Finite) Group Algebras

Periodicity of Random Walks on Finite Quantum Groups

The Ergodic Theorem for Random Walks: from Finite Groups, to Group Algebras, to Finite Quantum Groups

Finite Quantum Groups: Pure States

Introduction

Finite Ring Groups

Lemma 8.1

Lemma 8.2

Lemma 8.3

Lemma 8.4

Periodicity & Aperiodicity for Random Walks on Quantum Groups

Background

Ergodic Theorem for Random Walks on Finite Groups

Ergodic Theorem for Random Walks on Finite Quantum Groups

Irreducibility

Some Unresolved and Unexplored Aspects of Random Walks on Quantum Groups

“e in support” implies convergence

Total Variation Decrasing

Periodic $e^2$ is concentrated on a coset of a proper normal subgroup of $\mathfrak{G}_0$

Supported on Subgroup implies Reducible

Publication

Recent Comments

Categories

J.P. McCarthy Maths

Category Archive

Share this:

Share this:

Abstract

Share this:

Freslon’s Ergodic Theorem for (Finite) Group Algebras

Share this:

Share this:

Share this:

Introduction

Finite Ring Groups

Lemma 8.1

Lemma 8.2

Lemma 8.3

Lemma 8.4

Share this:

Background

Ergodic Theorem for Random Walks on Finite Groups

Ergodic Theorem for Random Walks on Finite Quantum Groups

Irreducibility

Share this:

“e in support” implies convergence

Total Variation Decrasing

Periodic is concentrated on a coset of a proper normal subgroup of

Supported on Subgroup implies Reducible

Share this:

Share this:

Recent Comments

Categories

Periodic $e^2$ is concentrated on a coset of a proper normal subgroup of $\mathfrak{G}_0$