Idea and Intuition
Let  be a (usually finite) set of generators and
be a (usually finite) set of generators and  a (usually finite) set of relations between the generators. The generators at this point are indeterminates, and we will be momentarily vague about what is and isn’t a relation. We write (if it exists!)
a (usually finite) set of relations between the generators. The generators at this point are indeterminates, and we will be momentarily vague about what is and isn’t a relation. We write (if it exists!)  for the universal
for the universal  -algebra generated by generators
-algebra generated by generators  and relations
and relations  .
.
It has the following universal property. Suppose  . Let
. Let  be a
be a  -algebra with elements
-algebra with elements  that satisfy the relations
that satisfy the relations  , then there is a (unique) *-homomorphism
, then there is a (unique) *-homomorphism  mapping
mapping  . This map will be a surjective *-homomorphism
. This map will be a surjective *-homomorphism  (aka a quotient map and
(aka a quotient map and  a quotient of
a quotient of  .
.
If the  generate
generate  ,
,  , then
, then  is a surjective *-homomorphism.
is a surjective *-homomorphism.
My (highly non-rigourous, the tilde reminding of hand-waving) intuition for this object is that you collect all (really all, not just isomorphism classes, we want below ![C([0,1])](https://s0.wp.com/latex.php?latex=C%28%5B0%2C1%5D%29&bg=ffffff&fg=545454&s=0&c=20201002) and e.g.
and e.g. ![C([0,2]](https://s0.wp.com/latex.php?latex=C%28%5B0%2C2%5D&bg=ffffff&fg=545454&s=0&c=20201002) ) of
) of  -algebras
-algebras  generated by
generated by  generators satisfying the relations
generators satisfying the relations  and forming a “big direct sum/product thingy” out of all of them:
and forming a “big direct sum/product thingy” out of all of them:
 .
.
Then the *-homomorphism  given by the universal property is given by projection onto that factor (which is a surjective *-homomorphism, a quotient):
given by the universal property is given by projection onto that factor (which is a surjective *-homomorphism, a quotient):
 .
.
This intuition works well but we should give a brief account of things are done properly.
First off, not every relation will give a universal  -algebra. For example, consider
-algebra. For example, consider  and
and  . The problem here is one of norm. Recall our rough intuition from above. What is the norm on
. The problem here is one of norm. Recall our rough intuition from above. What is the norm on  , this big thing
, this big thing  ? It should be something like, where the norm of
? It should be something like, where the norm of  is
is  the supremum over the factors:
the supremum over the factors:

The first approach to show that  does not exist is to consider for each
does not exist is to consider for each  the
the  -algebra
-algebra ![A_\alpha=C([0,\alpha])](https://s0.wp.com/latex.php?latex=A_%5Calpha%3DC%28%5B0%2C%5Calpha%5D%29&bg=ffffff&fg=545454&s=0&c=20201002) which is singly-generated by the self-adjoint
which is singly-generated by the self-adjoint  . But the norm
. But the norm  in
in 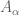 is the supremum norm, so we find
is the supremum norm, so we find  . From here:
. From here:

which is unbounded. The relations must give a bounded norm to the generators.
As an example of relations that do bound the generators, consider,  self-adjoint generators such that the sum of their squares is the identity:
self-adjoint generators such that the sum of their squares is the identity:
 .
.
These relations bounds the norm of the generators  1, and this gives existence to this algebra, using the Gelfand philosophy giving the “algebra of continuous functions on the free sphere”,
1, and this gives existence to this algebra, using the Gelfand philosophy giving the “algebra of continuous functions on the free sphere”,  (I think first considered by Banica and Goswami).
(I think first considered by Banica and Goswami).
Note here the relations are given by polynomial relations. If the polynomial relations are suitably admissible (i.e. give a bound to the generators), in this setting there is a real construction (real vs our ridiculous  ) of
) of  . See p.885 (link to *.pdf quantum group lecture notes of Moritz Weber).
. See p.885 (link to *.pdf quantum group lecture notes of Moritz Weber).
In fact, this is only a small class of the possible relations. I suggest there are at least two more types:
 relations that would be (admissible) norm relations (for example, in one generator, adding
relations that would be (admissible) norm relations (for example, in one generator, adding  , a non-polynomial relation, to the polynomial relation
, a non-polynomial relation, to the polynomial relation  gives an admissible set of relations, and
gives an admissible set of relations, and ![\mathrm{C}^*(g\mid g=g^*,\|g\|\leq 1)\cong C([-1,1])](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BC%7D%5E%2A%28g%5Cmid+g%3Dg%5E%2A%2C%5C%7Cg%5C%7C%5Cleq+1%29%5Ccong+C%28%5B-1%2C1%5D%29&bg=ffffff&fg=545454&s=0&c=20201002) . For
. For  /norm relations see here and maybe here.
/norm relations see here and maybe here.- (admissible) strong relations (see here for a use of this, with reference)
The constructions in one or both of cases might be constructive, as in the case (admissible) polynomial relations, but there is also an approach using category theory. But the main feature in all such definitions is the universal property, whose use could be summarised as follows:
Let  be a universal
be a universal  -algebra. The universal property can be used to answer questions about
-algebra. The universal property can be used to answer questions about  such as:
such as:
- is some polynomial
 in the generators non-zero,
in the generators non-zero,
- is
 infinite dimensional,
infinite dimensional,
- is
 non-commutative;
non-commutative;
because, if  is a
is a  -algebra with elements
-algebra with elements  that satisfy the relations then there is a unique *-homomorphism
that satisfy the relations then there is a unique *-homomorphism  . So, for example, where
. So, for example, where  is some such
is some such  then
then
- if
 , then
, then  as
as  ,
,
- if
 is infinite dimensional then
is infinite dimensional then 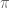 is a surjective *-homomorphism onto an infinite dimensional algebra, and so the domain
is a surjective *-homomorphism onto an infinite dimensional algebra, and so the domain  is infinite dimensional too.
is infinite dimensional too.
- if the commutator
![[f_i,f_j]\neq 0](https://s0.wp.com/latex.php?latex=%5Bf_i%2Cf_j%5D%5Cneq+0&bg=ffffff&fg=545454&s=0&c=20201002) , so that
, so that  is non-commutative, then so is
is non-commutative, then so is  as
as ![\pi([g_i,g_j])=[f_i,f_j]](https://s0.wp.com/latex.php?latex=%5Cpi%28%5Bg_i%2Cg_j%5D%29%3D%5Bf_i%2Cf_j%5D&bg=ffffff&fg=545454&s=0&c=20201002)
These quotients  can be considered models of
can be considered models of  .
.
Two Examples
A projection  in a
in a  -algebra is such that
-algebra is such that  . Consider
. Consider
 .
.
Existence is easy, because the norm of a non-zero projection is one. To answer questions about this algebra consider the infinite dihedral group  . This has group algebra
. This has group algebra  and group
and group  -algebra
-algebra  . Note that
. Note that  and
and 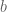 in
in  satisfy the relations of
satisfy the relations of  , and so we have a *-homomorphism (in fact a *-isomorphism)
, and so we have a *-homomorphism (in fact a *-isomorphism)  . This tells us that any monomial in the generators of
. This tells us that any monomial in the generators of  is non-zero,
is non-zero,  is infinite dimensional, and
is infinite dimensional, and  is non-commutative.
is non-commutative.
A partition of unity is a finite set of projections that sum to the identity,  . A magic unitary in a
. A magic unitary in a  -algebra
-algebra  is a matrix
is a matrix  such that the entries along any one row or column form a partition of unity. Consider (notation to be kept mysterious):
such that the entries along any one row or column form a partition of unity. Consider (notation to be kept mysterious):
 .
.
Consider the following magic unitary:
 .
.
Note that the  satisfy the relations of
satisfy the relations of  and in fact generate
and in fact generate  from above. Thus we have a quotient
from above. Thus we have a quotient  which shows that
which shows that  is infinite dimensional and noncommutative.
is infinite dimensional and noncommutative.
It is possible to show using a magic unitary with entries in  that for
that for  , a monomial with entries in
, a monomial with entries in 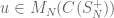 is zero for trivial reasons only (link to *.pdf, from Theorem 1 on).
is zero for trivial reasons only (link to *.pdf, from Theorem 1 on).
In addition it can be shown that for  (and similarly
(and similarly  ) the matrix in
) the matrix in  with
with  – entries
– entries

is a magic unitary, and thus by the universal property  is a *-homomorphism… the comultiplication giving
is a *-homomorphism… the comultiplication giving  the structure of a compact quantum group.
the structure of a compact quantum group.
Commutative Examples
If a universal  algebra is commutative (as in commutativity,
algebra is commutative (as in commutativity, ![[g_i,g_j]=0](https://s0.wp.com/latex.php?latex=%5Bg_i%2Cg_j%5D%3D0&bg=ffffff&fg=545454&s=0&c=20201002) , is one of the relations, vs the relations imply commutativity, as in
, is one of the relations, vs the relations imply commutativity, as in  (nice exercise)), we write
(nice exercise)), we write  . In this case Gelfand’s Theorem, that
. In this case Gelfand’s Theorem, that  , often allows us to easily identity the algebra (vs the noncommutative case where the universal algebra is mostly studied via models, quotients).
, often allows us to easily identity the algebra (vs the noncommutative case where the universal algebra is mostly studied via models, quotients).
Theorem
If  is a (polynomial) universal commutative
is a (polynomial) universal commutative  -algebra, then it of the form
-algebra, then it of the form  , and
, and  is given by the tuples
is given by the tuples  that satisfy the relations of of
that satisfy the relations of of  .
.
Proof: Characters are *-homomorphisms  .
.
Suppose that  satisfy the relations. Then by the universal property,
satisfy the relations. Then by the universal property,  is a *-homomorphism.
is a *-homomorphism.
On the contrary, suppose that 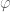 is a character. Then the relations are preserved under a *-homomorphism.
is a character. Then the relations are preserved under a *-homomorphism.
Examples
For  , projections in
, projections in 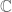 are just the scalars zero and one. Thus the spectrum is
are just the scalars zero and one. Thus the spectrum is  and
and 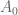 is the algebra of continuous functions on four points.
is the algebra of continuous functions on four points.
For  collect the tuple of
collect the tuple of 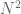 generators in a matrix. The relations imply that each such tuple is in fact a permutation matrix, and so the universal algebra above is the algebra of continuous functions on
generators in a matrix. The relations imply that each such tuple is in fact a permutation matrix, and so the universal algebra above is the algebra of continuous functions on  .
.
For

you end up with tuples of  real numbers in
real numbers in ![[-1,1]](https://s0.wp.com/latex.php?latex=%5B-1%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) whose sum of squares is one… otherwise known as the sphere
whose sum of squares is one… otherwise known as the sphere  .
.
Liberations
An interesting business here is to start with a universal commutative  algebra, say one of the three examples above… and see do you get something strictly bigger, necessarily non-commutative, if you drop commutativity. In the above, yes you do. Gelfand’s theorem says that a commutative unital
algebra, say one of the three examples above… and see do you get something strictly bigger, necessarily non-commutative, if you drop commutativity. In the above, yes you do. Gelfand’s theorem says that a commutative unital  -algebra is the algebra of continuous functions on a compact space
-algebra is the algebra of continuous functions on a compact space  (which we call a classical space). The Gelfand Philosophy says therefore that a noncommutative unital
(which we call a classical space). The Gelfand Philosophy says therefore that a noncommutative unital  -algebra
-algebra  can be thought of as the algebra of continuous functions on a compact quantum space
can be thought of as the algebra of continuous functions on a compact quantum space  . Note here
. Note here  is not a set-of-points, but a virtual object, and strictly
is not a set-of-points, but a virtual object, and strictly  is just notation (but see here).
is just notation (but see here).
Liberating the second example above from commutativity is the passage from the permutation group  to the quantum permutation group
to the quantum permutation group  . Liberating the third example above gives the passage from the real sphere
. Liberating the third example above gives the passage from the real sphere  to a quantum sphere called the free sphere
to a quantum sphere called the free sphere  .
.
We can also, of course, work in the other direction, imposing commutativity on not-necessarily universal  . If we write
. If we write  , then imposing commutativity gives us the classical version
, then imposing commutativity gives us the classical version  of
of  .
.
Imposing commutativity is not so scary: using the above you just get  … and everything we said above about identifying characters on
… and everything we said above about identifying characters on  holds for
holds for  too.
too.
This can be used: for example if a quantum group acts on a structure  , then its classical version acts on
, then its classical version acts on  . This idea was used by Banica and I to show that not every quantum permutation group is the quantum automorphism group of a finite graph (link to *.pdf).
. This idea was used by Banica and I to show that not every quantum permutation group is the quantum automorphism group of a finite graph (link to *.pdf).

Recent Comments