MATH7021: Spring 2024, Week 2

January 25, 2024 in MATH7021 | Leave a comment

Week 2

We finished the Gaussian Elimination examples on Thursday, and also began to look at applications of linear systems to traffic and pipe flow (Thursday).

We had good tutorial time… Monday, Wednesday, and a lot of the Thursday double too.

Week 3

We will start the week with the Monday tutorial and an additional tutorial on Tuesday

  • A207, Tuesday 30 January, 13:00-14:00

This is to make up somewhat for the two bank holiday Mondays.

We will finish the Chapter 1 material on Wednesday and Thursday and finish the week off with more tutorial time.

15% Assignment 1

Assignment 1 has a (provisional) hand-in date of Thursday 22 February (Week 5). See Canvas.

Study

Please feel free to ask me questions about the exercises via email or even better on this webpage.

Student Resources

Please see the Student Resources tab on the top of this page for information on the Academic Learning Centre, etc..

MATH7016: Spring 2024, Week 1

January 19, 2024 in MATH7016 | Leave a comment

In the first instance, there is a challenge in that DME2A’s lab takes earlier in the week than I have ever had before. This means that sometimes we might have to rush, or go back and forwards, to do our best to have material covered so that DME2A’s lab can be fruitful for them. They also have their two Bank Holiday labs rescheduled (see below – this also affects DME2E).

Week 1

In Week 1, by briefly looking at a number of examples (many of which we have seen before), we had a review of some central ideas from approximation theory such as approximation, measurement error, accuracy & precision, iteration, convergence, error, etc.

To help DME2A, we looked ahead at the Euler Method,

Then we started looking at where ordinary differential equations come into Engineering. This will continue in Week 2.

In VBA we had a quick review lab, focusing on plotting, the use of a dashboard, and then basic structure of our code:

  • Define variables,
  • Give variables initial values (from a dashboard),

A do loop that:

  • prints the current values of (relevant) variables and
  • calculates the next values.

If you have not completed Lab 1 (p.117), I recommend that you do at least up to Debugging to get you back in the VBA groove.

Hopefully, the first MCQ results will be on Canvas on Monday.

Read the rest of this entry »

MATH7021: Spring 2024, Week 1

January 18, 2024 in MATH7021 | Leave a comment

Week 1

We started the first chapter on Linear Algebra. Essentially, for us, simultaneous equations. We looked at Gaussian Elimination including Partial Pivoting, which is required in the presence of rounding. We looked at all but one of the examples, but had no tutorial time.

Gaussian Elimination Tutor

If you download Maple (see Student Resources), there is a Maple Tutor that is easy to use and will help you with Gaussian Elimination. Open up Maple and go to Tools -> Tutors -> Linear Algebra -> Gaussian Elimination.

Week 2

We will have tutorial time on Monday, then finish the Gaussian Elimination examples on Wednesday, and maybe begin to look at applications of linear systems to traffic and pipe flow.

Assignment 1

Assignment 1 has a (provisional) hand-in in Week 5. More information next week once the class list has settled down.

Study

Please feel free to ask me questions about the exercises via email or even better on this webpage.

Student Resources

Please see the Student Resources tab on the top of this page for information on the Academic Learning Centre, etc..

MATH6040: Winter 2023, Week 11

December 4, 2023 in MATH6040, MATH6040 - Day | Leave a comment

Test 2

Hopefully these results can be released the week of 4 December.

Student Feedback

If you would like to give fully anonymous feedback on this module and my teaching please go here.

Week 11

We will nearly finished Chapter 4 by looking at Related Rates and starting Implicit Differentiation.

Wednesday tutorials were focussed on Chapter 3 but the Friday BioEng2 tutorial was the first of the revision tutorials.

Week 12

We will finish the manual and then start revision.

Week 13

We will have all classes scheduled up to and including 12 December. These will all be tutorials

Study

Please feel free to ask me questions about the exercises via email.

Student Resources

Please see  Student Resources for information on the Academic Learning Centre, etc.

MATH7019: Winter 2023, Week 11

December 1, 2023 in MATH7019 | Leave a comment

Assignment 2

Has been corrected, and can be viewed Friday 1 December and maybe two classes next week.

Student Feedback

If you would like to give fully anonymous feedback on this module and my teaching please go here.

Week 11

We had one final bit of stats tutorial time on Monday. Then we finished Chapter 4 in two and a half classes, so had the first of our revision tutorials on Friday.

Weeks 12 and 13 to 11 December

All classes go ahead:

Academic Learning Centre

I would urge anyone having any problems with material that isn’t being addressed in the tutorial communication to use the Academic Learning Centre. If you are a little worried about your maths this semester you need to be aware of this resource. You will get best results if you come to the helpers there with specific questions.

Student Resources

Please see the Student Resources tab on the top of this page for information on the Academic Learning Centre, etc.

Study

Please feel free to ask me questions about the exercises via email.

MATH6055: Winter 2023, Week 10

December 1, 2023 in MATH6055 | Leave a comment

Student Feedback

If you would like to give fully anonymous feedback on this module and my teaching please go here.

Study Plan

I am going to recommend at this point that you spend some time outside tutorials doing exercises. Ideally getting ahead of the following proposed schedule:

Mathematics Exam Advice

  • You don’t have to answer questions in order Q. 1, Q. 2, etc. If you know in advance the structure of the exam, you can decide in advance what questions you are doing first, second, etc. This is related to:
  • Read questions carefully. Don’t glance at a question and go off writing: take a moment to understand what you have been asked to do.
  • Don’t use tippex; instead draw a simple line(s) through work that you think is incorrect.

If you do have time at the end of the exam, go through each of your answers and ask yourself:

  1. have I answered the question that was asked?
  2. does my answer make sense? If no, write that on your script, and then try and fix your solution.
  3. check your answer (e.g. if you are looking at something general, look at a special case; substitute your solution into equations; check your answer against a rough estimate; or what a picture is telling you; etc.). If your answer is wrong, write that on your script, and then try and fix your solution.

Week 10

A bit of a turbo-charge to finish the material for the exam. We introduced logs as inverses of exponential functions. Then we looked at properties and computer science applications of logs.

Weeks 11 and 12 to 12 December

As per the above, we have a number of revision classes.

The good news is that we will be able to finish Chapter 4 and skim the mini-Chapter 5 and still have everything well covered for assessment.

Academic Learning Centre

Have you heard about Maths Online on Canvas? It’s full of helpful Maths and Stats resources, notes, quizzes and videos to help you throughout the whole year. 

 We also use the Maths Online module on Canvas to offer Maths and Stats support to you and answer as many student questions as possible. 

Please log on to Maths online to book a maths appointment, book a place in a supported maths study session or request a workshopLinks to an external site..

 Supported Maths Study is on every Monday from 3.30pm – 5.30pm in B231.

Supported Statistics Study is on every Wednesday from 3pm – 4pm in B231.

 If you have any other question about our Maths and Stats supports email us on Academic.Learning@mtu.ie 

Student Resources

Please see the Student Resources tab on the top of this page for information on the Academic Learning Centre, etc.

Measuring a continuous observable

November 27, 2023 in C*-Algebras & Operator Theory, Research | Leave a comment

I am or rather was interested in the following problem: while we cannot hope to measure with infinite precision in the real world, in the mathematical world can I measure a continuous-spectrum self-adjoint operator given a fixed state? That is measure it with infinite precision?

Let A=:C(\mathbb{X}) be a unital \mathrm{C}^*-algebra, and \varphi\in\mathcal{S}(C(\mathbb{X})) a state on it… actually I will use the Gelfand–Birkhoff picture:

\varphi\in \mathbb{X} \iff \varphi\in\mathcal{S}(C(\mathbb{X}))

Note that 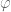\varphi has an extension to a \sigma-weakly continuous state \omega_\varphi on the bidual, C(\mathbb{X})^{**}. The algebra C(\mathbb{X}) sits isometrically in the bidual: the bidual as a von Neumann algebra contains the spectral projections of any self-adjoint f\in C(\mathbb{X}). We use the notation \mathbf{1}_E(f) for Borel E\subseteq\sigma(f).

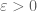Let \varepsilon> 0. Define:

p_\varepsilon(f)=\mathbf{1}_{(\lambda-\varepsilon,\lambda+\varepsilon)}(f).

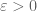Suppose for a state \varphi\in\mathbb{X} that for all \varepsilon>0:

\omega_\varphi(p_\varepsilon(f))>0.

(the situation where \omega_\varphi(p_\varepsilon(f))=0 will be moot).

Then we want to consider the entity:

\displaystyle \varphi_\lambda(g)=\lim_{\varepsilon\to0^+}\frac{\omega_\varphi(p_\varepsilon(f)gp_\varepsilon(f))}{\omega_\varphi(p_\varepsilon(f)}\qquad (g\in C(\mathbb{X})).

If this limit exists then it is a state.

Alas, this limit does not exist in general. There is a commutative counterexample by Nik Weaver on MO, which we will share here.

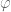Let A=L^{\infty}([0,1]) and f\in A given by f(x)=x and \varphi integration against Lesbesgue measure. Let 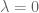\lambda=0 and p_{\varepsilon}=\mathbf{1}_{[0,\varepsilon)}.

Define

\displaystyle S=\bigcup_{n=0}^{\infty} [10^{-(2n+1)},10^{-2n}],

and g=\mathbf{1}_S, an element of L^{\infty}([0,1]).

Consider \varphi_0(g) and let \varepsilon =10^{-2m}, with m\in \mathbb{N}. It is possible to show that in this case:

\displaystyle \frac{\varphi(p_\varepsilon gp_\varepsilon)}{\varphi(p_\varepsilon)}=\frac{90}{99}.

However, at \varepsilon=10^{-(2m+1)}, we get 1/99. This means that the limit \varphi_0 above does not exist.

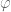Now, without proof we could expect that for A=C([0,1]), and the same f and \varphi, we could expect that in fact \varphi_0 exists, and \varphi_0(g)=g(0).

The problem here is that for L^{\infty}([0,1]), functions that disagree on a set of measure zero are identified and in general g(0) does not make sense for g\in L^\infty([0,1]).

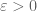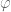The best we can do is measure f\in C(\mathbb{X}) up to tolerance \varepsilon>0. Say we measure f\in(\lambda-\varepsilon,\lambda+\varepsilon) with a state \varphi\in \mathbb{X}. Then we get conditioning of \varphi to a state:

\displaystyle \varphi_{\lambda,\varepsilon}(g)=\frac{\varphi(p_{\varepsilon}gp_{\varepsilon})}{\varphi(p_{\varepsilon})}\qquad (g\in C(\mathbb{X}))

In the commutative case, this is giving the average of 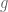g on the interval (\lambda-\varepsilon,\lambda+\varepsilon).

I had hoped to use \varphi_\lambda to explain why classical spheres don’t admit quantum symmetry. Alas the above means my argument probably cannot work (well, maybe I can use the \varepsilon of room?)

Perhaps we could try and understand in which \mathrm{C}^*-algebras the state \varphi_\lambda is well-defined… but we can say at least for today that we cannot measure continuous observables with infinite precision… even mathematically.

MATH6040: Winter 2023, Week 10

November 26, 2023 in MATH6040, MATH6040 - Day | Leave a comment

Test 2

Test 2 is booked for the Wednesday of Week 11:

29/11/202318.00-19.00MATH6040Technological Maths 20160+A – D

See Canvas —> MATH6055 —> Assignments, for more information, including sample tests.

Student Feedback

If you would like to give fully anonymous feedback on this module and my teaching please go here.

Week 10

We looked at applications of partial differentiation to error analysis. Then we started looking at parametric differentiation.

The tutorials will again be focused on Chapter 3.

Week 11

We will hopefully finish Chapter 4 by looking at Related Rates and Implicit Differentiation.

Wednesday tutorials are focussed on Chapter 3 but the Friday BioEng2 tutorial will be the first of the revision tutorials.

Week 12

We will finish the manual and then start revision.

Students will receive one-to-one help in tutorial, but it will be up to students to decide what they want to look at; be it Vectors, Matrices, or Further Differentiation.

Students who don’t know what to do might be invited to look at the exam paper at the back of the manual.

Week 13

We will have all classes scheduled up to and including 12 December. These will all be tutorials

Tutorials

The most important thing in your MATH6040 world is to attend tutorials regularly.

If BioEng2B students genuinely cannot make the Friday tutorial, they may come to the BioEng2A tutorial at 3 pm on Wednesdays in B260. This can continue as long as the number of students in that tutorial stays at 20 or below.

Study

Please feel free to ask me questions about the exercises via email.

Student Resources

Please see  Student Resources for information on the Academic Learning Centre, etc.

MATH7019: Winter 2023, Week 10

November 24, 2023 in MATH7019 | Leave a comment

Assignment 2 — DUE TODAY FRIDAY 24 November

Assignment 2 based on Chapter 2 is on Canvas now: Canvas —> MATH7019 —> Assignments.

Student Feedback

If you would like to give fully anonymous feedback on this module and my teaching please go here.

Week 10

We looked at hypothesis testing. There was a tutorial on sampling on Wednesday, and a little tutorial time for full exam questions on Thursday and then more tutorial time on Friday.

Week 11

We will have one final bit of tutorial time on Monday. Then we have three classes to try and see can we finish Chapter 4. If we don’t we have two more classes in Week 12. The second part of Chapter 4 is actually second year material. The first part is Euler’s Method: done.

Any classes left over in these five classes will be revision tutorials. Then we have another four review classes which will be given over to tutorial time.

Academic Learning Centre

I would urge anyone having any problems with material that isn’t being addressed in the tutorial communication to use the Academic Learning Centre. If you are a little worried about your maths this semester you need to be aware of this resource. You will get best results if you come to the helpers there with specific questions.

Student Resources

Please see the Student Resources tab on the top of this page for information on the Academic Learning Centre, etc.

Study

Please feel free to ask me questions about the exercises via email.

MATH6055: Winter 2023, Week 9

November 24, 2023 in MATH6055 | Leave a comment

Student Feedback

If you would like to give fully anonymous feedback on this module and my teaching please go here.

15% Test 2

Results have been released on Canvas.

For the solutions, go to Canvas —> MATH6055 —> Assignments —> COMP1C Test 2

Study Plan

I am going to recommend at this point that you spend some time outside tutorials doing exercises. Ideally getting ahead of the following proposed schedule:

Week 9

We will spent time on equations and spent time talking about indices/exponentials.

In tutorial, C-X looked at Sample Test 2, and C-Y moved onto functions. We are very short for time for tutorials: students are advised to spend some time outside tutorials working on exercises.

Week 10

There is going to be a bit of a turbo-charge to finish the material for the exam. We will introduce logs as inverses of exponential functions. Then we will be looking at properties and computer science applications of logs.

The good news is that we will be able to skim the mini-Chapter 5 and still have everything well covered for assessment.

We have two lectures in Week 11. Then we have four more classes of review which will also be tutorials.

Academic Learning Centre

Have you heard about Maths Online on Canvas? It’s full of helpful Maths and Stats resources, notes, quizzes and videos to help you throughout the whole year. 

 We also use the Maths Online module on Canvas to offer Maths and Stats support to you and answer as many student questions as possible. 

Please log on to Maths online to book a maths appointment, book a place in a supported maths study session or request a workshopLinks to an external site..

 Supported Maths Study is on every Monday from 3.30pm – 5.30pm in B231.

Supported Statistics Study is on every Wednesday from 3pm – 4pm in B231.

 If you have any other question about our Maths and Stats supports email us on Academic.Learning@mtu.ie 

Student Resources

Please see the Student Resources tab on the top of this page for information on the Academic Learning Centre, etc.