Here we present the proof of the following theorem:
Let be functions that are differentiable at some
. If
, then
is differentiable at
with
Quotient Rule
Remark: In the Leibniz notation,
Proof: Let :
Letting on both sides:
Last year's maths is easy, this year's maths is hard and next year's maths is impossible.
Here we present the proof of the following theorem:
Let be functions that are differentiable at some
. If
, then
is differentiable at
with
Quotient Rule
Remark: In the Leibniz notation,
Proof: Let :
Letting on both sides:
5 comments
Comments feed for this article
May 30, 2011 at 11:55 am
jim kelly
There is a far easier way to do the quotient rule using delta x
May 30, 2011 at 12:30 pm
J.P. McCarthy
Jim,
Far easier?? Care to elaborate? Surely the difference is just cosmetic?
J.P.
May 30, 2011 at 6:29 pm
J.P. McCarthy
Jim,
I presume this is it:
Click to access easyway.pdf
I have to say I like this method — moreover it works for the sum rule also.
Thank you,
J.P.
August 29, 2013 at 7:15 pm
Student 46
Hi J.P,
I used the quotient rule to find to find the critical points and this gave me
to find the critical points and this gave me
What do I need to do next?
August 29, 2013 at 7:23 pm
J.P. McCarthy
Critical points are points such that so you want
so you want
Now the only time that a fraction is equal to zero is when the top (numerator) is zero.
Therefore we want
It is difficult to see when a sum is zero but easy to see when a product is zero by the No-Zero-Divisors-Theorem which says that if and
and 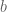 are two numbers and
are two numbers and 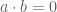 then either
then either 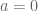 or
or 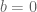 . So we want to write the above as a product… we must factorise. What is common to both… the
. So we want to write the above as a product… we must factorise. What is common to both… the 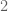 and
and  :
:
These are the critical points. They might be maxima or minima (or neither — won’t happen on your paper). To do this we test them at the second derivative which is the derivative of the first derivative:
Now evaluate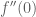 and
and  .
.
If is a critical point then
is a critical point then
Regards,
J.P.