Project Maths: A More Geometric Approach to De Moivre’s Theorem and Complex Roots

Introduction

This is just a short note to provide an alternative way of proving and using De Moivre’s Theorem. It is inspired by the fact that the geometric multiplication of complex numbers appeared on the Leaving Cert Project Maths paper (even though it isn’t on the syllabus — lol). It assumes familiarity with the basic properties of the complex numbers.

Complex Numbers

Arguably, the complex numbers arose as a way to find the roots of all polynomial functions. A polynomial function is a function that is a sum of powers of $x$ . For example, $q(x)=x^2-x-6$ is a polynomial. The highest non-zero power of a polynomial is called it’s degree. Ordinarily at LC level we consider polynomials where the multiples of $x$ — the coefficients — are real numbers, but a lot of the theory holds when the coefficients are complex numbers (note that the Conjugate Root Theorem only holds when the coefficients are real). Here we won’t say anything about the coefficients and just call them numbers.

Definition

Let $a_n,\,a_{n-1},\,\dots,\,a_1,\,a_0$ be numbers such that $a_n\neq 0$ . Then

$p(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0$ ,

is a polynomial of degree $n$ .

In many instances, the first thing we want to know about a polynomial is what are its roots. The roots of a polynomial are the inputs $x$ such that the output $p(x)=0$ .

Definition

A number $k$ is a root of a polynomial $p$ if and only if $p(k)=0$ .

The roots of $2x^3-13x^2+13x+10$ are where the graph cuts the $x$ -axis at $-1/2,\,2$ and $5$ .

It didn’t take long for 16th century mathematicians to realise that some polynomials with real coefficients had roots that could be expressed with such fantastical quantities as $\sqrt{-15}$ . They showed that these polynomials had solutions if the ‘ficticious quantity’ $i=\sqrt{-1}$ was allowed. These polynomials were fairly simple but not as simple as $q(x)=x^2+1$ . Consider the roots of $q$ :

$x^2+1=0\Rightarrow x^2=-1\Rightarrow x=\pm\sqrt{-1}$ .

If we want to be able to solve all polynomials we need complex numbers — and the Fundamental Theorem of Algebra says that the complex numbers are enough — we don’t need stranger and stranger types of numbers to find the roots of polynomials.

Definition

A complex number is a number of the form $a+bi$ where $a,\,b\in\mathbb{R}$ . We denote the set of complex numbers by $\mathbb{C}$ .

The addition and multiplication of complex numbers can just be defined in the natural way:

$(a+bi)+(c+di)=(a+c)+(b+d)i$

$(a+bi)(c+di)=ac+adi+bci+bdi^2=ac-bd+(ad+bc)i$ .

There is essentially nothing wrong with this but the Argand Diagram hints at a more geometric realisation of complex numbers. The Argand Diagram is a plane where the complex number $a+ib$ is represented by the coordinate $(a,b)$ :

The complex number $3+4i$ represented on the Argand Diagram

Now there is another way to look as complex numbers — as vectors with a magnitude (distance from the origin) and direction (angle made with the positive real-axis).

A quick application of Pythagoras Theorem shows that the magnitude, $r$ , of a complex number $z=a+bi$ , is given by $\sqrt{a^2+b^2}$ (also denoted by $|z|$ ). The angle, or argument, of $z$ is harder to write a single definition for but in this case $\theta\in(0,\pi/2)$ is given by $\theta=\tan^{-1}(b/a)$ .

This implies that instead of writing $z=a+bi$ or even $z=(a,b)$ , we could write $z=(\text{magnitude},\text{argument})=(r,\theta)$ . These are called polar coordinates — while the ‘normal’ coordinates are called cartesian coordinates (i.e. $z=(a,b)$ ). Suppose we know that a complex number is given in polar coordinates by $z=(r,\theta)$ — what is this in cartesian coordinates? That is, suppose $z=a+bi$ — what are $a,\,b\in\mathbb{R}$ ?

Take the sine and cosine of $\theta$ .

We have that

$\sin\theta=\frac{b}{r}\Rightarrow b=r\sin\theta$ , and

$\cos\theta=\frac{a}{r}\Rightarrow a=r\cos\theta$ .

Thus $z=a+bi$ is given by:

$z=r\sin\theta+ir\cos\theta=r(\sin\theta+i\cos \theta)$ .

Just to be safe, we should make sure that if $z=r(\cos\theta+i\sin \theta)$ , then $|z|=r$ and $\text{Arg}(z)=\theta$ . That $|z|=r$ is a straightforward exercise, and that $\text{Arg}(z)=\theta$ is clear from the definition of sine and cosine.

Multiplication of Complex Numbers

As mentioned above, we can define the multiplication of complex of numbers in a very natural way. Consider the complex numbers $1,i,i^2,i^3,i^4$ . By definition, $i^2=-1$ ; therefore $i^3=i\times i^2=-i$ ; and $i^4=i^2\times i^2=(-1)(-1)=1$ .

Multiplying $i$ by $i^k$ is the same by rotating through the right angle $\pi/2$ . Does this work for other numbers? Suppose $z$ has argument $\theta$ ; is $iz$ found by rotating through $\pi/2$ ?

The answer to this is YES. Algebraic multiplication of complex numbers corresponds to rotation in the geometric picture. To be precise, if $z_1$ is a complex number with argument $\theta$ , and $z_2$ is a complex number with argument $\alpha$ , then the argument of $z_1\times z_2$ is $\theta$ — plus a rotation through an angle $\alpha$ — i.e. the argument of $z_1z_2$ is $\theta+\alpha$ .

What about the magnitude of $z_1,\,z_2$ ? Luckily, the situation is the same as for real numbers — if $x,\,y\in\mathbb{R}$ , then we have

$|xy|=|x||y|$ .

To show that $|z_1z_2|=|z_1||z_2|$ is a standard exercise in cartesian coordinates; here we give our main result where this fact is showed even more straightforwardly.

Proposition

Suppose that $z_1$ has magnitude $r$ and argument $\theta$ ; and $z_2$ has magnitude $s$ and argument $\alpha$ . Then the product of $z_1$ and $z_2$ has magnitude $r\times s$ and argument $\theta+\alpha$ .

Proof : We simply compute:

$z_1z_2=r(\cos\theta+i\sin\theta)\times s(\cos\alpha+i\sin\alpha)$ ,

$=rs(\cos\theta+i\sin\theta)(\cos\alpha+i\sin\alpha)$ ,

$=rs(\cos\theta\cos\alpha+i\cos\theta\sin\alpha+i\sin\theta\cos\alpha-\sin\theta\sin\alpha)$ ,

$=rs(\cos\theta\cos\alpha-\sin\theta\sin\alpha+i(\cos\theta\sin\alpha+\sin\theta\cos\alpha))$ .

Now note the identities:

$\cos(A+B)=\cos A\cos B-\sin A\sin B$ ,

$\sin(A+B)=\cos A\sin B+\sin A\cos B$ .

Therefore

$z_1z_2=rs(\cos(\theta+\alpha)+i\sin(\theta+\alpha))$ .

That is $z_1z_2$ has magnitude $rs$ and argument $\theta+\alpha$ $\bullet$

In other words, we can simplify the multiplication of complex numbers to

$(r,\theta)\times(s,\alpha)=(rs,\theta+\alpha)$ .

A lot more elegant in my opinion than the standard approach!

Remarks

Note that if we multiply together complex numbers $z_1=(r,\theta)$ and $z_2=(s,\alpha)$ such that $\theta+\alpha>2\pi$ , we can just take out multiples of $2\pi$ as $\sin(x+2k\pi)=\sin x$ and $\cos(x+2k\pi)=\cos x$ for $k\in\mathbb{Z}$ . Compare this with $i^5$ . We can see from the Argand Diagram that $i$ has argument $\pi/2$ so multiplying by $i$ four more times will add a rotation of $\pi/2$ each time yielding $\text{Arg}(i^5)=\pi/2+2\pi$ . But of course this is just equivalent to $\pi/2$ — and once we note that $|i|=1$ we have that $i^5$ must equal $i$ .

Given a complex number in cartesian coordinates $z=a+ib$ ; its conjugate is defined as $\bar{z}=a-ib$ . Again we can think of conjugates geometrically; taking conjugates corresponds to changing the sign of the imaginary part of $z$ — convince yourself that this is the same as symmetry in the $y$ -axis:

The conjugate of $z=(r,\theta)$ is given by $(r,-\theta)$ .

Now if you multiply $\bar{z}$ by $z$ , you rotate $\bar{z}$ through an angle $\theta$ bringing it onto the real axis. This explains why a complex number multiplied by its conjugate is a real number. It is clear that

$z\bar{z}=(r,\theta)(r,-\theta)=(r^2,0)= r^2\in\mathbb{R}$ .

We can also derive a nice expression of the division of $z_1=(r,\theta)$ by the non-zero $z_2=(s,\alpha)$ (note that $z=(r,\theta)=0+0i$ if and only if $r=0$ ). Now

$\frac{z_1}{z_2}=z_1\times\frac{1}{z^2}=z_1z_2^{-1}$ .

Now $z^{-1}$ is just that number that when multiplied by $z=(r,\theta)$ yields $1$ . Geometrically it is clear that $\text{Arg}(z^{-1})=-\theta$ . Alternatively we solve the equation

$(r,\theta)\times (x,y)=(1,0)\Rightarrow (rx,\theta+y)=(1,0)$ ,

which has the unique (mod $2\pi$ in argument) solution

$z^{-1}=(\frac{1}{r},-\theta)$ .

Hence we have

$\frac{z_1}{z_2}=\frac{(r,\theta)}{(s,\alpha)}=\left(\frac{r}{s},\theta-\alpha\right)$ .

De Moivre’s Theorem

This work makes De Moivre’s Theorem very straightforward indeed.

De Moivre’s Theorem for Natural Number Powers

Suppose that $z=(r,\theta)$ and $n\in\mathbb{N}$ . Then

$z^n=(r^n,n\theta).$

Proof : Well, this isn’t really necessary — it really is obvious with the work done above.

$z^n=\underbrace{z\times z\times\cdots\times z}_{n\text{ times}}$ ,

$\Rightarrow z^n=(r\times r\times \cdots\times r,\theta+\theta+\cdots+\theta)=(r^n,n\theta)$ $\bullet$

De Moivre’s Theorem for Integer Powers

Suppose that $z=(r,\theta)$ and $n\in\mathbb{Z}$ . Then

$z^n=(r^n,n\theta).$

Proof : The case of $n\geq 1$ is covered by the last theorem. If $n=0$ we need

$z^0=(r^0,0\theta)$ .

But $z^0=1$ , $r^0=1$ and $0\theta=0$ so we just have to show

$1=(1,0)$ ,

which is true (draw a diagram).

Now suppose $n<0$ , say $n=-m$ for $m\in\mathbb{N}$ .

$z^{n}=z^{-m}=\frac{1}{z^m}=\frac{(1,0)}{(r^m,m\theta)}$ .

We have seen already seen how to do division:

$\frac{(1,0)}{(r^m,m\theta)}=\left(\frac{1}{r^m},0-m\theta\right)=(r^{-m},-m\theta)=(r^n,n\theta)$

as required $\bullet$

Example 2007 Paper I, Q.3 (b)(i)

Let $z=-1+i$ , where $i^2=-1$ . Use De Moivre’s Theorem to evaluate $z^5$ and $z^9$ .

Solution

Write $z$ in polar form. A quick sketch and calculation shows that

$z=(\sqrt{2},3\pi/4)$

$\Rightarrow z^5=(\sqrt{2}^5,15\pi/4)=(4\sqrt{2},7\pi/4)$ ,

$\Rightarrow z^9=(16\sqrt{2},27\pi/4)=(16\sqrt{2},3\pi/4)$ .

Roots of Unity

Recall the set of complex numbers $\{1,i,-1,-i\}$ — which can be written in polar form $\{(1,0),(1,\pi/2),(1,\pi),(1,3\pi/2)\}$ . What happens when we take any of these to the power of four?

$(1,0)^4=(1^4,4(0))=1$ ,

$(1,\pi/2)^4=(1,4\pi/2)=(1,2\pi)=(1,0)=1$ ,

$(1,\pi)^4=(1,4\pi)=(1,0)=1$ ,

$(1,3\pi/2)^4=(1,4(3\pi/2))=(1,6\pi)=(1,0)=1$ .

So these are all numbers such that when we raise them to the power of four, we get one — that is they are fourth roots of $1$ . A good question at this point is to ask are there any more complex numbers $z=a+ib=(r,\theta)$ such that $z^4=1$ ? The natural setting for this question is back in the algebra picture — it is a deep theorem that every complex polynomial has a root. Now we can use the factor theorem:

Factor Theorem

Suppose that $p:\mathbb{C}\rightarrow\mathbb{C}$ is a polynomial. Then $k\in\mathbb{C}$ is a root of $p$ if and only if $(z-k)$ is a factor of $p$ .

Proof : Here $\bullet$

The fact that a polynomial $p$ has a root $k\in\mathbb{C}$ implies that we can then (after polynomial long division) write it in the form

$p(z)=(z-k)q(z)$ ,

where $q(z)$ is another polynomial, whose degree is one less than that of $p$ . Inductively, we then have:

Fundamental Theorem of Algebra

Suppose that $p:\mathbb{C}\rightarrow \mathbb{C}$ is a polynomial of degree $n$ . Then $p$ can be written in the form

$p(z)=c(z-\alpha_1)(z-\alpha_2)\cdots(z-\alpha_n)$ .

Moreover, the $\alpha_i$ are the roots of $p$ .

How is this relevant to the fourth powers of 1? Well finding solutions to $z^4=1$ is equivalent to finding roots of the polynomial $z^4-1$ . The Fundamental Theorem of Algebra guarantees that there are only four such roots — hence if we find four we know that there are no more! We will use this fact in the sequel: roots can be repeated, but if we find $n$ distinct solutions of a degree $n$ polynomial, we know that there are no more solutions.

Now we can get back to roots of unity. We now know that the $q$ th roots of unity are solutions of the equation

$z^q=1$ .

Let $z=(r,\theta)$ :

$(r,\theta)^q=(r^q,q\theta)\overset{!}{=}(1,0).$

Now $r\geq0$ so the only solution to $r^q=1$ is $r=1$ . Now which angles are such that

$q\theta\equiv 0\text{ mod }2\pi$ ?

Well this is the same as saying

$q\theta=2k\pi$ for $k\in\mathbb{Z}$ ,

$\theta=\frac{2k\pi}{q}$ for $k\in\mathbb{Z}$ .

So let’s us try $k=0,1,2,\dots,q-1$

$\theta=0,\,\frac{2\pi}{q},\,\frac{4\pi}{q},\,\frac{6\pi}{q},\dots,\frac{2(q-1)\pi}{q}.$

We know there are no more solutions as the $q$ solutions are the $q$ roots of the degree $q$ polynomial

$p(z)=z^k-1$ .

In fact all of this can be neatly appreciated in a picture:

Consider all of these complex numbers brought to the power of eight ( $45^\circ=\pi/4$ ):

$(1,k\pi/4)^8=(1,8\frac{k\pi}{4})=(1,2k\pi)=(1,0)$ .

Hence to find all the $q$ -th roots of unity it suffices to draw the unit circle, divide equally into $q$ sectors and these are the $q$ -roots!

Note from our multiplication that the $q$ -th roots of unity are the $q$ powers of the what we might call the principal $q$ -th root of unity $\xi_q:=\frac{2\pi}{q}$ :

$(1,2\pi/q)^k=(1,2k\pi/q)$ for $k=0,1,2,\dots,q-1$ .

Complex Roots: De Moivre’s Theorem for Fractional Powers

It can also be shown that DeMoivre’s Theorem holds for fractional powers. This is to solve equations such as

$z^3=3-3i$ .

In a certain sense, this is the same as solving $z=(3-3i)^{1/3}$ ; and we can use De Moivre’s Theorem to find $z$ . Suppose that $z=(r,\theta)$ and we want the $q$ -th root of $z$ . Using De Moivre’s Theorem we get the principal root of $(r\theta)$ :

$(\sqrt[q]{z},\text{Arg}(z)/q)$

However there are three roots of the polynomial $z^3-(3-3i)$ so there should be three solutions. Where are they? Instead I propose a much slicker way of solving these equations. I write:

$z^3=(1)(3-3i)$

$z=\{\xi^k_3(3-3i)^{1/3}:k=0,1,2\}$ ,

where $\xi_3$ is the principal cube root of unity and $(3-3i)^{1/3}$ is the principal root of $3-3i$ . A quick sketch of $3-3i$ and calculation shows that $(3-3i)=(3\sqrt{2},7\pi/4)$ . A root is a solution of the equation:

$(r,\theta)^3=(\sqrt{18},7\pi/4)$ ,

$(r^3,3\theta)=(\sqrt{18},7\pi/4)$ ,

$\Rightarrow ((18^{1/2})^{1/3},7\pi/12)$ .

Now the trick is that

$\xi^k(\sqrt[6]{18},7\pi/12)$ for $k=0,1,2$

are three distinct solutions to the equation — hence three distinct roots of the degree three polynomial — and therefore they are all of them.

Hence the solutions of $z^q=w$ are:

$\{\xi_q(\sqrt[q]{|w|},\text{Arg}(w)/q)\,:\,k=0,1,2,\dots,q-1\}$ .

Example: 2007 Paper I, Q 3(c)(i)

Find the two complex numbers $a+bi$ for which $(a+ib)^2=15+8i$ .

Solution

We need to find the two square roots of $15+8i$ . The two square roots of $1$ are $\pm 1$ . Now we need to write $15+8i$ in polar form to find it’s principal square root. Now a quick sketch and calculation shows that

$15+8i=(17,\tan^{-1}(8/15))$ .

Hence the principal root of $15+8i$ is $(\sqrt{17},\tan^{-1}(8/15)/2)$ . Now multiply by the two square roots of unity to get the two square roots of $15+8i$ are

$\pm(\sqrt{17},\tan^{-1}(8/15)/2)$ .

3 comments

Comments feed for this article

November 19, 2011 at 3:33 pm

Project Maths: A More Geometric Approach to De Moivre's Theorem …

[…] link: Project Maths: A More Geometric Approach to De Moivre's Theorem … CLICK HERE for “Learning Multiplication & Division – Reference […]

November 21, 2015 at 1:18 pm

Pupil

Had to solve the equation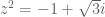 $z^2=-1+\sqrt{3}i$ and answer in rectangular form. Book doesn’t have answers.

November 21, 2015 at 1:35 pm

J.P. McCarthy

The first issue is that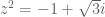 $z^2=-1+\sqrt{3}i$ is a quadratic (like $x^2$ and so has TWO solutions.

You have only one. Knowing that a quadratic has TWO solutions (which can be equal!) helps when solving equations such as

$x^2=12$ .

If you take the square root of both sides:

$x=\sqrt{12},$

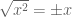you only get one solution. There are two solutions — where is the other? You can solve it cheaply by knowing that a quadratic has two solutions… ah, $-\sqrt{12}$ is the other (by the way the problem in taking the square root of both sides is that $\sqrt{x^2}=\pm x$ — $+x$ if $x$ is positive and $-x$ if $x$ is negative (e.g. $\sqrt{(-2)^2}=\sqrt{4}=2=-(-2)$ ))!

So there are two solutions and that is the number one problem.

Here we give two solutions — the first is more general.

Solution 1: O.K., we have

$\displaystyle z^2=2(\cos(2\pi/3)+i\sin(2\pi/3))$ .

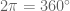Now the thing is that $\cos$ and $\sin$ are periodic with period $2\pi=360^\circ$ . This means that

$\cdots\cos(2\pi/3-2\pi)=\cos(2\pi/3)=\cos(2\pi/3+2\pi)$
$=\cos(2\pi/3+4\pi)=\cos(2\pi/3+6\pi)+\cdots$

and so we actually have

$\displaystyle z^2=2\left(\cos(2\pi/3+2k\pi)+i\sin(2\pi/3+2k\pi)\right)$

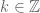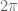where $k\in\mathbb{Z}$ and so $2k\pi=k(2\pi)$ are ‘multiples of $2\pi$ /full revolutions’.

Now if we apply De Moivre we get:

$\displaystyle z=\sqrt{2}\left(\cos(\pi/3+k\pi)+i\sin(\pi/3+k\pi)\right)$ ,

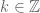for $k\in\mathbb{Z}$ .

Each $k$ gives a solution.

$k=0$ :

$\displaystyle z=\sqrt{2}(\cos \pi/3+i\sin\pi/3)=\sqrt{2}(1/2+i\sqrt{3}/2)=\frac{\sqrt{2}}{2}+i\frac{\sqrt{6}}{2}$ .

$k=1$ :

$\displaystyle z=\sqrt{2}(\cos(\pi/3+\pi)+i\sin(\pi/3+\pi))=\sqrt{2}(\cos 4\pi/3+i\sin 4\pi/3)$
$\displaystyle =\sqrt{2}(-1/2-i\sqrt{3}/2)=-\frac{\sqrt{2}}{2}-i\frac{\sqrt{6}}{2}$ .

$k=2$ : …. well $k=2$ will give the same solution as $k=0$ … moreover the quadratic has only two solutions and we have two so we are done. The solution set is

$\displaystyle \pm\left(\frac{\sqrt{2}}{2}+i\frac{\sqrt{6}}{2}\right)$ .

Solution 2 — only works for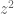 $z^2$ really.

Do what you did to get
$\displaystyle z_1=\frac{\sqrt{2}}{2}+i\frac{\sqrt{6}}{2}$ .

Note that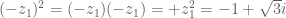 $(-z_1)^2=(-z_1)(-z_1)=+z_1^2=-1+\sqrt{3}i$ also and so is also a solution. There are only two solutions because it is a quadratic and because we have found two we are done.

To understand this in more depth read the above piece.

Regards,
J.P.

	J.P. McCarthy on Leaving Cert Maths: A Pro…
	J.P. McCarthy on You Can’t Get a Negative…
	J.P. McCarthy on MATH6038: Week 4*
	Sean O'Reilly on MATH6038: Week 4*
	J.P. McCarthy on MATH7019: Week 11

Project Maths: A More Geometric Approach to De Moivre’s Theorem and Complex Roots

Introduction

Complex Numbers

Definition

Definition

Definition

Multiplication of Complex Numbers

Proposition

Remarks

De Moivre’s Theorem

De Moivre’s Theorem for Natural Number Powers

De Moivre’s Theorem for Integer Powers

Example 2007 Paper I, Q.3 (b)(i)

Solution

Roots of Unity

Factor Theorem

Fundamental Theorem of Algebra

Complex Roots: De Moivre’s Theorem for Fractional Powers

Example: 2007 Paper I, Q 3(c)(i)

Solution

Recent Comments

Categories

J.P. McCarthy Maths

3 comments

Leave a Reply Cancel reply

Project Maths: A More Geometric Approach to De Moivre’s Theorem and Complex Roots

Introduction

Complex Numbers

Definition

Definition

Definition

Multiplication of Complex Numbers

Proposition

Remarks

De Moivre’s Theorem

De Moivre’s Theorem for Natural Number Powers

De Moivre’s Theorem for Integer Powers

Example 2007 Paper I, Q.3 (b)(i)

Solution

Roots of Unity

Factor Theorem

Fundamental Theorem of Algebra

Complex Roots: De Moivre’s Theorem for Fractional Powers

Example: 2007 Paper I, Q 3(c)(i)

Solution

Share this:

Like this:

Related

Recent Comments

Categories

J.P. McCarthy Maths

3 comments

Leave a Reply Cancel reply