I am emailing a link of this to everyone on the class list every week. If you are not receiving these emails or want to have them sent to another email address feel free to email me at jpmccarthymaths@gmail.com and I will add you to the mailing list.
Review Tutorial/Lecture
Wednesday 1 May at 10:00 in WGB G014.
Feedback
Thank you for your feedback today.
I would make the following comments:
The Homework is hard but fair: ye are final year students. Also I have repeatedly said that I am willing to answer questions about it.
It has everything to do with what we are doing in class (iterator functions, fixed points, orbits, etc.) and ye are supposed to know about the other topics from other modules.
I agree that it might require a lot of thought for 12.5% but when you are finished with it I have no doubt whatsoever that your understanding of the material can only be increased.
More exercise sheets? Agreed — although I didn’t see much evidence of us doing the too-few questions that I was posing weekly.
Regarding getting your tests back: ye have an option to view them but I need to keep them I’m afraid.
Tutorials
Summer 2012: Question 4 (e), (f)
Autumn 2012: Question 4 (d), (f)
Math.Stack Exchange
If you find yourself stuck and for some reason feel unable to ask me the question you could do worse than go to the excellent site math.stackexchange.com. If you are nice and polite, and show due deference to these principles you will find that your questions are answered promptly. For example this question on the Tent Mapping.
Week 12
We summarised our work on roots of unity and illustrated the following result… parts 4 & 5 are not examinable so don’t worry that it wasn’t covered in lectures. In fact as it turned out the proof was a lot harder than I thought… it is not true for all — only for almost all irrational
when
as far as I know ! The following proposition is true though.
Proposition
Suppose that is a power mapping
for some
.
Then the dynamical system exhibits the following behaviours:
- If
then
.
- If
then
- If
with
then
is eventually periodic.
Suppose now that . Then
4. If with
for, in binary,
Then has a dense orbit.
(In fact, is a chaotic mapping.)
5. Suppose now that and we are again looking at
. Then there exists an
such that the orbit of
is not dense in
.
Proof: The proof of statement 4. is essentially the same as that of that of the doubling mapping (the bottom of p.55 top of p.56 in the notes).
The proof of 5. goes as follows:
Let and let
be the (proper) subset of
of irrational numbers containing only
s and
s in their base-
expansion. If we take
we then have that
and so can not be dense in
when


12 comments
Comments feed for this article
May 15, 2013 at 2:14 pm
Student 41
I was just wondering for question four part of the exam in the past exam papers is there any examples online which provides clear examples how to find the fixed points, period-2 points and eventually fixed point of a function such as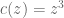 ? I am struggling a bit with this and the Argand diagram part.
? I am struggling a bit with this and the Argand diagram part.
May 15, 2013 at 2:28 pm
J.P. McCarthy
I suppose it’s too late to say that we did them in class…
O.K. go back to what you know. What is a fixed point of a function: a point that is sent to itself by the iterator function. In this case we are looking for points such that
such that
We need to solve this equation. It matters what the set of states is but I am going to suppose that it is the whole of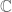 and therefore we can say that there should be three solutions (why). There are probably two ways to solve this:
and therefore we can say that there should be three solutions (why). There are probably two ways to solve this:
1. Quick but Dangerous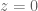 is a fixed point as
is a fixed point as  . Now suppose that
. Now suppose that  so we can divide both sides by
so we can divide both sides by  :
:
Note that
The solutions of this are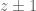 . Hence the fixed points are
. Hence the fixed points are  .
.
2. Safer
Rewrite as
at .
.
For the period-2 points we want to find points such that when we apply the iterator function twice we can back to where we started:
That is
This time we should use the second method. We should expect nine solutions (why?). Get everything equal to zero:
So we either want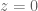 or
or  . These are the 8th roots of unity. The way to find them is to note that the complex number
. These are the 8th roots of unity. The way to find them is to note that the complex number  is an 8th-root (why). All of the other roots are powers/rotations of this primitive root:
is an 8th-root (why). All of the other roots are powers/rotations of this primitive root:
8th-roots of unity are
Hence the nine period-2 points are .
.
More on roots of unity here (http://en.wikipedia.org/wiki/Root_of_unity).
You will have to be a bit more specific in telling me what part of the the Argand diagram you are struggling with:
1. A complex number is located at the coordinate
is located at the coordinate 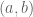 .
. has an argument (angle with the positive real-axis) of
has an argument (angle with the positive real-axis) of  and is located at a distance of
and is located at a distance of  from the origin.
from the origin.
2. A complex number
To find an eventually fixed point of an iterator function you are looking for a point that is eventually (in a finite number of steps) sent to a fixed point. In this case,
that is eventually (in a finite number of steps) sent to a fixed point. In this case,
where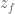 is a fixed point.
is a fixed point.
Regards,
May 21, 2013 at 11:31 am
John Whooley
Hi J.P, Could you show me how to show points like e^3(pi)i/4 are attracting or repelling or nuetral? I am a little bit stuck with this. Thanks
May 21, 2013 at 3:02 pm
J.P. McCarthy
John,
This question is meaningless without reference to an iterator function. If is a differentiable function then
is a differentiable function then 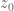 is an attracting fixed point if
is an attracting fixed point if 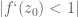 etc
etc
Regards,
J.P.
May 16, 2013 at 8:34 pm
Student 42
I have a few questions regarding the MS3011 Dynamical Systems Exam.
For Question two I have all the proofs for Logistic Mappings and Doubling but have no proof/theorem for Tent Mapping. Is the theory for this section about the conditions of it which are 0<u<4 etc.
As regards the Complex Number section I have all the class written notes but seem to be missing typed notes in my booklet. Do you by any chance have an online PDF or e-copy for this section?
Finally are there solutions for the 2012 Autumn Question 3 and 4 and the Continuous Assessment Exam available?
May 16, 2013 at 8:41 pm
J.P. McCarthy
First of all we are only taking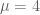 for the Tent Mapping and call this
for the Tent Mapping and call this  . I suppose the questions that I could ask about the Tent Mapping include how many period-
. I suppose the questions that I could ask about the Tent Mapping include how many period- points does
points does  have, show that the periodic points are dense and show that any fraction is eventually periodic under
have, show that the periodic points are dense and show that any fraction is eventually periodic under  .
.
Does your typeset notes stop at page 8 of the complex numbers section? Then you are not missing anything: I threw out a lot of the complex number stuff.
To your final question no and no — although we did all of the Autumn 2012 questions in the lectures and the CA test material is very straigtforward. However a word of caution: learning off answers is no good to ye now: ye need to understand the material.
Regards,
J.P.
May 17, 2013 at 12:10 pm
linda crowley
With regard to doubling mapping question in autumn 2009 paper. ‘What do you expect the graph of D^n to look like?’ Am i correct in saying it will have 2^n lines… Im also wondering how to find how many fixed points D^n has?
May 17, 2013 at 2:41 pm
J.P. McCarthy
Linda,
Yes you are correct to say that has
has 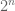 lines.
lines.
A fixed point of a function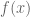 is found at the intersection of
is found at the intersection of  and
and  . Therefore draw a schematic (rough) graph of
. Therefore draw a schematic (rough) graph of  with its
with its 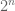 lines and
lines and  . How many times does
. How many times does  intersect the graph of
intersect the graph of  ?
?
A second, more algebraic, solution is as follows. A fixed point of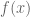 is a point that is sent to itself
is a point that is sent to itself
Hence fixed points of are solutions of
are solutions of
in other words period- points. We know that the period-
points. We know that the period- points are points of the form (why?)
points are points of the form (why?)
and there are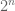 of these (why?), hence
of these (why?), hence  has
has 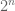 fixed points.
fixed points.
Regards,
J.P.
May 17, 2013 at 4:08 pm
Aoife
The logistic family of mappings in Summer 2011 Q 2, part (c) ask to find the fixed points when an infection enters the population in terms of /mu and the mortality rate. Do I just alter the equation to
in Summer 2011 Q 2, part (c) ask to find the fixed points when an infection enters the population in terms of /mu and the mortality rate. Do I just alter the equation to 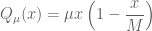 where
where  is my mortality rate and then solve for my fixed points? And also what does
is my mortality rate and then solve for my fixed points? And also what does 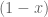 mean in terms of the population growth model?
mean in terms of the population growth model?
May 18, 2013 at 3:44 pm
J.P. McCarthy
Aoife,
Call the mortality rate by . Note this is a different
. Note this is a different  to the one in the notes — which is the maximum population: more on this below. Therefore the equation governing the population growth is given by
to the one in the notes — which is the maximum population: more on this below. Therefore the equation governing the population growth is given by
You can solve then for the fixed points.
then for the fixed points.
Note that is the proportion of the maximum population: the population that, if reached, results in extinction. Therefore if
is the proportion of the maximum population: the population that, if reached, results in extinction. Therefore if 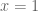 , i.e. at the maximum, then the next population is
, i.e. at the maximum, then the next population is
The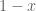 term models this.
term models this.
Regards,
J.P.
May 21, 2013 at 2:42 pm
Student 43
Given a real valued function
f(x)= x +sin x
How do you show that f(x) has an infinite number of fixed points?
May 21, 2013 at 3:05 pm
J.P. McCarthy
How do you find fixed points?
Regards,