I am emailing a link of this to everyone on the class list every week. If you are not receiving these emails or want to have them sent to another email address feel free to email me at jpmccarthymaths@gmail.com and I will add you to the mailing list.
Homework
Will be discussed in class on Monday.
Week 10
On Monday we showed that to multiply one complex number by another
involves stretching
by a factor of
and then rotating through an angle
. On Tuesday we used this information to find roots of unity. We also spoke about the Conjugate Root Theorem.
Week 11
More on complex numbers including De Moivre’s Theorem and taking roots.
Exercises
For the Week 11 tutorial you should look at Q.54 and 61-63.
Math.Stack Exchange
If you find yourself stuck and for some reason feel unable to ask me the question you could do worse than go to the excellent site math.stackexchange.com. If you are nice and polite, and show due deference to these principles you will find that your questions are answered promptly. For example this conjecture about calculating .

2 comments
Comments feed for this article
March 18, 2014 at 3:57 pm
Student
Hi JP,
I just have a few questions regarding the homework,
When representing the conjugate of a complex number geometrically, is it acceptable to describe it as a rotation by the negative value of the original angle of the equation?
e.g. implies that
implies that  .
.
If the angle between and the
and the  -axis is 30 degrees, is the conjugate not just a rotation by -30 degrees as only the value of the imaginary number changes?
-axis is 30 degrees, is the conjugate not just a rotation by -30 degrees as only the value of the imaginary number changes?
For question 1 on the homework is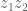 the product or the composition?
the product or the composition?
Thanks,
March 18, 2014 at 4:00 pm
J.P. McCarthy
Hi,
A better way of thinking would be to say that the conjugate of is the reflection of
is the reflection of  in the real (
in the real ( ) axis.
) axis.
If you were doing it using rotations, the conjugate would actually be a rotation of through an angle
through an angle  …
…
Regards,
J.P.