I am emailing a link of this to everyone on the class list every week. If you are not receiving these emails or want to have them sent to another email address feel free to email me at jpmccarthymaths@gmail.com and I will add you to the mailing list.
Continuous Assessment
You are identified by the last four digits of your student number unless you are winning the league. The individual quiz marks are out of 2.5 percentage points. Your best eight quizzes go to the 20% mark for quizzes. The R % column is your running percentage (for best eight quizzes), MPP is your Maple Percentage Points and the GPP is your Gross Percentage Points (for best eight quizzes and Maple). Most of the columns are rounded but column six, for quiz five, is correct.
| S/N | Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Q7 | Q8 | Q9 | Q10 | Q11 | R % | QPP | MPP | GPP |
| Kelliher | 3 | 3 | 3 | 3 | 2.3 | 98 | 12.3 | 4.5 | 16.8 | ||||||
| 8335 | 2 | 3 | 2 | 3 | 2.5 | 98 | 12.3 | 4.5 | 16.8 | ||||||
| 3281 | 2 | 3 | 3 | 3 | 2.1 | 96 | 12.0 | 4.5 | 16.5 | ||||||
| 5527 | 2 | 3 | 3 | 3 | 2.5 | 94 | 11.9 | 4.5 | 16.4 | ||||||
| 7878 | 2 | 2 | 2 | 2 | 2.1 | 85 | 10.6 | 4.5 | 15.1 | ||||||
| 8416 | 2 | 1 | 2 | 3 | 2.5 | 84 | 10.5 | 4.5 | 15.0 | ||||||
| 8478 | 2 | 2 | 2 | 2 | 0 | 82 | 8.2 | 4.5 | 12.7 | ||||||
| 1864 | 1 | 2 | 3 | 2 | 1.24 | 76 | 9.5 | 4.5 | 14.0 | ||||||
| 8403 | 2 | 1 | 2 | 3 | 1.3 | 76 | 9.5 | 4.5 | 14.0 | ||||||
| 4198 | 0 | 1 | 2 | 3 | 1.7 | 74 | 7.4 | 4.5 | 11.9 | ||||||
| 6548 | 2 | 1 | 2 | 3 | 1.6 | 71 | 8.9 | 4.5 | 13.4 | ||||||
| 8603 | 1 | 2 | 2 | 2 | 0 | 67 | 6.7 | 3 | 9.7 | ||||||
| 8556 | 1 | 1 | 2 | 2 | 0 | 66 | 6.6 | 4.5 | 11.1 | ||||||
| 2567 | 2 | 2 | 2 | 1 | 1.8 | 65 | 8.2 | 4.5 | 12.7 | ||||||
| 1852 | 1 | 1 | 2 | 2 | 2.1 | 57 | 7.1 | 4.5 | 11.6 | ||||||
| 2859 | 2 | 1 | 0 | 1 | 1.6 | 55 | 5.5 | 4.5 | 10.0 | ||||||
| 5546 | 0 | 0 | 1 | 1 | 1.9 | 53 | 4.0 | 4.5 | 8.5 | ||||||
| 7950 | 0 | 0 | 1 | 0 | 1.8 | 52 | 2.6 | 3 | 5.6 | ||||||
| 9464 | 1 | 1 | 2 | 1 | 1.24 | 46 | 5.7 | 4.5 | 10.2 | ||||||
| 7209 | 2 | 1 | 2 | 1 | 0.16 | 44 | 5.5 | 4.5 | 10.0 | ||||||
| 8455 | 0 | 1 | 1 | 1 | 1.9 | 38 | 4.8 | 4.5 | 9.3 | ||||||
| 4775 | 1 | 0 | 1 | 0 | 0.4 | 22 | 2.2 | 4.5 | 6.7 | ||||||
| 5553 | 0 | 1 | 0 | 0 | 0.1 | 17 | 1.3 | 4.5 | 5.8 |
Any students who missed a Maple lab are invited to do the lab in their own time. What you must do is take the Maple file and get through all of the exercises. When completed email me a copy of your Maple worksheet. Expect to take a good deal longer than an hour to complete. Note if you do this I will give you your 1.5% for that lab.
Here we do the Question 2 Questions.
2 i.
Determine .
Solution: We have
.
The middle term needs a product rule:
.
2 ii.
Determine .
Solution: This requires a quotient rule:
.
2 iii.
Determine .
Solution: Using the chain rule and the product rule (and the chain rule therein):
.
Quiz 6 Question Bank
The question bank for Quiz 6 (in Week 8) is as follows:
- P.65 Q. 2,3 and 4 (take the error in C to be 0)
- P.75 Q. 1-4, 7*-8
*answer should be rather than
.
There is no value in writing down the final answers alone — you will receive marks for full and correct solutions — but nothing for final answers without justification or skipping important steps. Please don’t learn off model solutions — you need to understand the material not just on a superficial level to do well later on. Quiz 6 runs from 19:00 to 19:15 sharp on Wednesday 25 March.
Academic Learning Centre
The word on the Academic Learning Centre is that although the evening session perhaps might have been made exclusive to evening students, the fact of the matter is that they are not.
My departmental head suggested that if a group of ye want to get an improvement in your ALC experience, that ye should email questions to catherine.palmer@cit.ie in advance of the session. Dr Palmer said that this will allow her to more easily help ye.
Week ‘6’
Remember we have a ‘Maple night’ on April 1 in the normal rooms.
Maple Labs
We next have a Maple Lab Wednesday 1 April. Group 1 – Starts at 18:00 and Finishes at 20:50: Wednesdays 18:00-19:05 – Maple Lab in room C219 Wednesdays 19:15-19:30 – Weekly Quiz in C212 Wednesdays 19:30-20.50 – Theory class in room C212 Group 2 – Starts at 19:15 and Finishes at 22:00: Wednesdays 19:15-19:30 – Weekly Quiz in C212 Wednesdays 19:30-20:50 – Theory class in room C212 Wednesdays 20.55-22:00 – Maple Lab in room C219 As you can see here you can download a student copy of Maple. Some students said that they were unable to open the file I sent in their Maple 17 — this is strange as I am actually using Maple 16!
Week 7
In Week 7 we finished off Error Analysis and started looking at some numerical methods of solving equations. In Maple, we looked at Partial Differentiation and Error Analysis.
Week 8
In Week 8 we will finish off looking at the Newton Raphson Method and learn how to numerically approximate integrals.We might start the final chapter.
Study
Please feel free to ask me questions about the exercises via email or even better on this webpage. Anyone can give me exercises they have done and I will correct them. I also advise that you visit the Academic Learning Centre.
Continuous Assessment
The Continuous Assessment is broken into Weekly Quizzes (20%) and Maple (10%). There will be eleven weekly quizzes and your eight best results will count (so 2.5% per quiz from eight quizzes). You will receive an email (i.e. this one) on Thursday/Friday detailing the examinable exercises. Maple consists of five labs and a Maple Test in the sixth lab. Satisfactory participation in labs gives you 1.5% and the Maple Test is worth 2.5%. More on this in the coming days.
Student Resources
Please see the Student Resources tab on the top of this page for information on the Academic Learning Centre, etc..

4 comments
Comments feed for this article
March 23, 2015 at 8:51 pm
Fintan Connolly
Hi J.P, on Question 3. Page 65 I keep ending up with 0.05 as my error instead of 0.5. Would you be able to run down the question a bit, I have my calculator set to radians also.
March 24, 2015 at 8:54 am
J.P. McCarthy
Fintan,
I am not sure exactly what you are doing wrong without seeing what you did. There are three things that might have gone wrong. Firstly your differentiation. To differentiate
you need the quotient rule as it is a fraction. Let me do the derivative with respect to :
:
The next thing you might have done is not used the absolute values:
Finally the partial derivatives must be evaluated at the measurements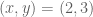 .
.
If this doesn’t help you might send me a photo of your work.
Regards,
J.P.
March 24, 2015 at 8:55 am
Student
Hey J.P.,
I have a few questions for you. For questions on p.65 do you ignore the minus sign when you’re looking for the error?
On p.75 can you get more than one answer when looking for the root?
Thanks.
March 24, 2015 at 9:05 am
J.P. McCarthy
Yes you ignore the sign error as you don’t want errors to cancel: you take the worse case scenario.
For example, if is some quantity that depends on variables
is some quantity that depends on variables  and
and  , then the error in the calculation of
, then the error in the calculation of 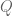 due to errors in the measurement of
due to errors in the measurement of  and
and  (
( and
and  ) is given by:
) is given by:
The absolute values mean that you change negative numbers to positive and leave positive:
Regarding the second question, yes it doesn't matter 'what' side you bring the terms to. For example, you have
and say
Now if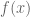 has a root at
has a root at  then
then 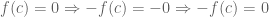 , i.e.
, i.e.  also has a root at
also has a root at  .
.
Regarding the final answer, note I say in the question that I only want you to find the approximate location of ONE of the roots: there can be more than one. In general, anything with an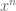 will have
will have  roots.
roots.
To see this particular example I can use Wolfram Alpha (or Maple of course) to plot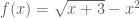 :
:
http://www.wolframalpha.com/input/?i=Plot%5B%28x%2B3%29%5E%281%2F2%29-x%5E2%2C%7Bx%2C-3%2C3%7D%5D
Regards,