I am emailing a link of this to everyone on the class list every week. If you are not receiving these emails or want to have them sent to another email address feel free to email me at jpmccarthymaths@gmail.com and I will add you to the mailing list.
Manuals
You will need to purchase the manual from the CIT Copy Centre beside the Student Centre (in the same room as where you get your photos taken for your student card). Note that this is a cash-free area so you will need to put the appropriate amount of funds on your student card.
The Copy Centre will be open until 19:30 the first and second weeks of the term but from next week goes back to normal opening hours — closing at 16:30.
Quiz 1 Results and Solutions
Below find the results. You are identified by the last four digits of your student number unless you are excelling. The marks are out of 2.5 percentage points. Your best eight quizzes go to the 20% mark for quizzes. The R % column is your running percentage (for best eight quizzes). One student didn’t write down their name. They should email me. Solutions and marking scheme here.
| S/N | Quiz 1 | R% |
| Fahey | 2.5 | 100 |
| Buckley | 2.5 | 100 |
| Nolan | 2.43 | 97.2 |
| 8332 | 2.37 | 94.8 |
| 8212 | 2.37 | 94.8 |
| 1486 | 2.24 | 89.6 |
| 8426 | 2.24 | 89.6 |
| 2128 | 2.24 | 89.6 |
| 9464 | 2.17 | 86.8 |
| 6645 | 2.17 | 86.8 |
| 9896 | 1.97 | 78.8 |
| 2237 | 1.71 | 68.4 |
| 3481 | 1.71 | 68.4 |
| 2942 | 1.71 | 68.4 |
| 3703 | 1.71 | 68.4 |
| 1321 | 1.45 | 58 |
| 7879 | 1.12 | 44.8 |
| 2073 | 0.99 | 39.6 |
| 9555 | 0.53 | 21.2 |
| Not registered but did test. | 0.53 | 21.2 |
| 2257 | 0.53 | 21.2 |
| 7209 | 0.39 | 15.6 |
| 8354 | 0.39 | 15.6 |
| 2070 | 0.33 | 13.2 |
| 3872 | 0.26 | 10.4 |
| 2092 | 0 | 0 |
| 1298 | ? | |
| 4402 | ? | |
| 8425 | ? |
Quiz 2 Question Bank
Question bank for Quiz 2 (in Week 3) is as follows:
- P.26, Q. 1 (a), (b), (d), 2(a), 3, 6
- P.35, Q.1-4, 7,8, 10
If you have any specific difficulties with these questions, please email me. Alternatively use Maple or Wolfram Alpha to help. Your Quiz 2 Questions will be taken from these. The final answers will not be given on the quiz paper and neither is there any value in writing down the final answers alone — you will receive marks for full and correct solutions — but nothing for final answers without justification or skipping important steps. No hints will appear either. Please don’t learn off model solutions — you need to understand the material not just on a superficial level to do well later on.
Quiz 2 runs from 19:15 to 19:30 sharp on Wednesday 15 February.
Maple Labs
Due to the fact that there are more than 20 students attending the module MATH6037 Mathematics for Science 2.1, we will have to introduce a lab split starting this week, on Wednesday 15 February.
The Maple Lab takes place in C128.
The 15 individuals who responded to the poll and wanted to start at 18:00 (below) are guaranteed a spot in the early sitting. If there is space for more they can be accommodated, otherwise they have to start at 19:15 and do Maple at 20:55. Note there is a smaller class for the later Maple. If you are struggling with Maple you could consider switching to the later class to get more attention.

The following is the proposed schedule for Weeks 3, 5, 7, 8, 10, 11:
Group 1 – Starts at 18:00 and Finishes at 20:50:
Wednesdays 18:00-19:05 – Maple Lab in room C219
Wednesdays 19:15-19:30 – Weekly Quiz in C212
Wednesdays 19:30-20.50 – Theory class in room C212
Group 2 – Starts at 19:15 and Finishes at 22:00:
Wednesdays 19:15-19:30 – Weekly Quiz in C212
Wednesdays 19:30-20:50 – Theory class in room C212
Wednesdays 20.55-22:00 – Maple Lab in room C219
In weeks where there is no Maple Lab, the quiz will take place from 19:00-19:15 sharp.
Week 2
In Week 2 we looked at -substitutions. Then we studied Integration by Parts: this is the start of the new material (i.e. not MATH6019 material).
Week 3
We will start Partial Differentiation which we will use to do Error Analysis.
In Maple we will do some basic plotting, differentiation and integration.
Plan
- Week 3: Maple Lab 1 & Section 1.4
- Week 4: Section 1.4 & Section 1.5
- Week 5: Maple Lab 2 & Section 2.1
- Week 6: Section 2.2 & Sections 3.1-3.3
- Week 7: Maple Lab 3 & Sections 3.1-3.3
- Week 8: Maple Lab 4 & Section 3.4
- Week 9: Section 3.4
- Week 10: Maple Lab 5 & Section 3.4
- ————-EASTER————–
- Week 11: Maple Test & Section 3.4
- Week 12: Section 3.5
- ————-END OF LECTURES———-
- Week 13: Review Class — Summer 2015 Paper
Academic Learning Centre
I would urge anyone having any problems with the material to use the Academic Learning Centre. You will get best results if you come to the helpers there with specific questions.
Study
Please feel free to ask me questions about the exercises via email or even better on this webpage. Anyone can give me exercises they have done and I will correct them. I also advise that you visit the Academic Learning Centre.
Continuous Assessment
The Continuous Assessment is broken into Weekly Quizzes (20%) and Maple (10%). There will be eleven weekly quizzes and your eight best results will count (so 2.5% per quiz from eight quizzes). You will receive an email (i.e. this one) on Thursday/Friday detailing the examinable exercises. Maple consists of five labs and a Maple Test in the sixth lab. Satisfactory participation in labs gives you 1.5% and the Maple Test is worth 2.5%. More on this in the coming days.
Student Resources
Please see the Student Resources tab on the top of this page for information on the Academic Learning Centre, etc..

8 comments
Comments feed for this article
February 13, 2017 at 9:45 am
Student
Why in the question is shown and then you change it to
is shown and then you change it to 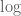 ,when these are two completely different buttons on the calculator.
,when these are two completely different buttons on the calculator.
Regards.
February 13, 2017 at 9:47 am
J.P. McCarthy
I should have kept to to avoid this confusion.
to avoid this confusion.
In a calculus context, usually means
usually means 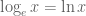 rather than
rather than  .
.
Regards,
J.P.
February 14, 2017 at 8:26 am
Student
Sorry to bother you again J.P. but how is the integral of 1/2 equal to 1/4?
Thanks.
February 14, 2017 at 8:28 am
J.P. McCarthy
You are dealing with
The constant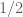 can be taken out to give
can be taken out to give
Regards,
J.P.
February 14, 2017 at 8:29 am
Student
Hi J.P.,
I’m having a bit of difficulty with Q. 1(a) p. 26. I was just wondering would you bring over the line before substituting
over the line before substituting  or leave it under the line?
or leave it under the line?
Regards.
February 14, 2017 at 8:33 am
J.P. McCarthy
You have two options.
Forgetting about the limits for the moment and only doing the antiderivative.
If you first let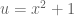 you should end up with:
you should end up with:
Now you need to use
and then antidifferentiate.
Alternatively you can do that manipulation first to get
and then carry out the substitution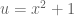 .
.
You will get the same antiderivative and hence integral in both cases.
Regards,
J.P.
February 15, 2017 at 10:35 am
Student
J.P.,
I’m doing Q. 1, p.35. I know the basics of the question but I’m a little rusty on using the table… am I right in saying I’m looking for the anti-derivative of ???
???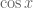 …. how did you know which table to look at here.
…. how did you know which table to look at here.
In the solutions you point towards using
I see where you get it from. Is the table on the left differentiation only and the table in the middle anti-differentiation?
Cheers.
February 15, 2017 at 10:45 am
J.P. McCarthy
Your problem might be one of notation.
Suppose we have a function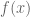 .
.
If we want to denote “the derivative of with respect to
with respect to  ” we write
” we write  .
.
Therefore, the left-hand table has on its left functions and on its right derivatives of those functions with respect to .
.
For example, if then
then  .
.
On the other hand, if we want to denote “the anti-derivative of with respect to
with respect to  ” we write
” we write
The denotes anti-differentiation but we also need the
denotes anti-differentiation but we also need the  to say we are anti-differentiating with respect to
to say we are anti-differentiating with respect to  .
.
In MATH6037,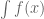 on its own is meaningless. We need the
on its own is meaningless. We need the  to tell us what we are differentiating with respect to.
to tell us what we are differentiating with respect to.
Therefore, the right-hand hand table has on its left functions and on its right anti-derivatives of those functions with respect to .
.
For example, if then
then  .
.
Regards,
J.P.