Quiz 6 Results
Below find the results. Your best eight quizzes go to the 20% mark for quizzes. The R % column is your running percentage (for best eight quizzes). The QPP is your Quiz Percentage Points (a max of 19.5 at the moment). MPP is your Maple percentage points. GPP is your gross percentage points.
| S/N | Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | R% | QPP | MPP | GPP/19.5 |
| 1298 | 0.6 | 0.8 | 1.6 | 47.3 | 7.1 | 3 | 10.1 | |||
| 2327 | 2.5 | 1.9 | 1.4 | 74.8 | 11.2 | 4.5 | 15.72 | |||
| 2073 | 2.5 | 2.5 | 2.5 | 89.9 | 13.5 | 4.5 | 17.99 | |||
| 8332 | 0.6 | 1.9 | 2.5 | 73.9 | 11.1 | 4.5 | 15.59 | |||
| 9464 | 1.8 | 2.1 | 2.5 | 90.5 | 13.6 | 4.5 | 18.07 | |||
| 4402 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 3872 | 1.2 | 0 | 1.4 | 35.7 | 5.36 | 4.5 | 9.86 | |||
| 1480 | 1.5 | 2.5 | 2.3 | 89.1 | 13.4 | 4.5 | 17.87 | |||
| 2237 | 0 | 1.2 | 1.4 | 35.3 | 5.29 | 4.5 | 9.79 | |||
| 2070 | 2.3 | 2.5 | 2.5 | 66 | 9.9 | 4.5 | 14.4 | |||
| 3481 | 1.5 | 2.4 | 2.3 | 61.7 | 9.25 | 4.5 | 13.75 | |||
| 3703 | 1.4 | 2.3 | 2.5 | 73.1 | 11 | 4.5 | 15.46 | |||
| 7879 | 2.2 | 1.5 | 2.4 | 64.8 | 9.72 | 4.5 | 14.22 | |||
| 2257 | 1.2 | 1.6 | 1.8 | 49.8 | 7.47 | 4.5 | 11.97 | |||
| 8425 | 1 | 1.8 | 2.4 | 48.2 | 7.23 | 4.5 | 11.73 | |||
| 9896 | 0 | 0 | 0 | 13.1 | 1.97 | 0 | 1.97 | |||
| 8212 | 2.5 | 2.5 | 2.5 | 96.3 | 14.4 | 4.5 | 18.94 | |||
| 1486 | 0 | 2.5 | 0 | 47.6 | 7.14 | 1.5 | 8.64 | |||
| 5484 | 1 | 1.9 | 2.5 | 85.5 | 12.8 | 4.5 | 17.33 | |||
| 1321 | 1.02 | 1.2 | 1.9 | 44.9 | 6.73 | 4.5 | 11.23 | |||
| 2128 | 2.5 | 2.3 | 1.5 | 74.8 | 11.2 | 4.5 | 15.72 | |||
| 2942 | 1.8 | 1.8 | 2.5 | 75 | 11.3 | 4.5 | 15.75 | |||
| 6645 | 2.5 | 2.5 | 2.5 | 97.8 | 14.7 | 4.5 | 19.17 | |||
| 8426 | 0 | 1.2 | 2.5 | 56.3 | 8.44 | 3 | 11.44 | |||
| 2092 | 0.2 | 0 | 1.6 | 12 | 1.8 | 3 | 4.8 | |||
| 8354 | 0.2 | 1.7 | 1.9 | 29.4 | 4.41 | 4.5 | 8.91 |
Maple Lab
The Maple Lab takes place in C128.
The following is the proposed schedule for Weeks 9, 11, 12:
Group 1 – Starts at 18:00 and Finishes at 20:50:
Wednesdays 18:00-19:05 – Maple Lab in room C128
Wednesdays 19:15-19:30 – Weekly Quiz in C212
Wednesdays 19:30-20.50 – Theory class in room C128
Group 2 – Starts at 19:15 and Finishes at 22:00:
Wednesdays 19:15-19:30 – Weekly Quiz in C128
Wednesdays 19:30-20:50 – Theory class in room C212
Wednesdays 20.55-22:00 – Maple Lab in room C128
In weeks where there is no Maple Lab, the quiz will take place from 19:00-19:15 sharp.
Quiz 7
Quiz 7 will contain two questions — a main question and a bonus question.
The main question will be harder than the bonus question:
or
.
The main question will be worth 2.5%.
If the main question is too difficult you can instead do the bonus question which is worth 1.5%. The bonus question will be
or some other constant,
(e.g.
.
Both the main question and the bonus question will be marked and your highest score will count (so you can’t do the bonus question and a bit of the main question and add the marks).
If you learn off a solution and you skip steps I will heavily punish you. This question is worth 2.5% (if you do the main question) but worth a lot more in the final exam. There is no point learning off a solution, getting the 2.5% now and not getting the 6.3% available in the exam for this question. Try and be able to think your way through the question… something like this:
OK, I need to use the formula to find the Laplace Transform from first principles… formula… it’s on the paper:
Right… to calculate infinite integrals I integrate up to a large number
…
To calculate integrals I need to anti-differentiate:
Is this direct from the tables? Does it need a manipulation? U-substitution? Integration by parts? If I find
[the anti-derivative depends on
and
]
I can find the integral by doing top limit minus bottom limit:
.
Finally I need to take the limit as
:
.
Quiz 6 runs from 19:15 to 19:30 sharp on Wednesday 29 March.
Week 8
We looked at Laplace Transforms — calculating from first principles and also using the table.
Week 9
We will continue working on Laplace Transforms and hopefully start talking about the inverse Laplace Transform.
Plan: Catch-up
We are going to get to Easter and then see how we are getting on. The following is a proposal that includes no catch up.
- Week 9: Maple Lab 4 & Section 3.4
- Week 10: Section 3.4
- ————-EASTER————–
- Week 11: Maple Lab 5 & Section 3.4
- Week 12: Maple Test & Section 3.5
- ————-END OF LECTURES———-
- Week 13: Review Class — Summer 2015 Paper
Maple Catch Up
If you want to do Maple catch up (if you miss a lab) you have two options:
- download the Maple file from your email, do the exercises in Maple (either in a new worksheet or on top of the original file with the exercises), save the worksheet and email me the worksheet you were working on.
- come in for a double Maple session on a ‘Maple’ night.
Academic Learning Centre
I would urge anyone having any problems with the material to use the Academic Learning Centre. You will get best results if you come to the helpers there with specific questions.
Study
Please feel free to ask me questions about the exercises via email or even better on this webpage. Anyone can give me exercises they have done and I will correct them. I also advise that you visit the Academic Learning Centre.
Student Resources
Please see the Student Resources tab on the top of this page for information on the Academic Learning Centre, etc..

2 comments
Comments feed for this article
March 31, 2017 at 7:29 am
Student
Hi J.P.,
With regards to Q. 1 (iii) can you tell me where that rule came from. I’m totally stumped and I’ve read your answer but it is still not clicking with me. Is it not a case of transforming by its own rule and
by its own rule and  by its rule?
by its rule?
March 31, 2017 at 7:39 am
J.P. McCarthy
No.
The only time you can transform term-by-term in that way is if you have a SUM. So, for example,
but things are more complicated with a PRODUCT, in particular,
There is NO product rule for Laplace Transforms EXCEPT for when you want to send — that is except when one of the functions you are transforming is an exponential.
— that is except when one of the functions you are transforming is an exponential.
When one of the functions is an exponential the First Shift(/Translation) Theorem applies. This states:
Let us break this down a little bit.
When the function is multiplied by an exponential in the time domain that has the effect of SHIFTING the function is the -domain.
-domain.
This shifting, which is a horizontal translation in the graph, has the effect of shifting to
to 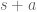 .
.
In laymen terms — well inasmuch as these can be made into laymen terms:
– The ‘ ‘ just means you transform
‘ just means you transform  as normal
as normal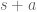 means that it isn’t evaluated at
means that it isn’t evaluated at  (e.g.
(e.g.  ) but at
) but at 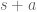 (e.g.
(e.g.  ).
).
– The
So in the case of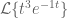 you transform the
you transform the  as normal… but then shift the
as normal… but then shift the  to
to  .
.
It can be hard to write this down. I suggest transform the first:
first:
and then shift the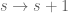 :
:
Regards,
J.P.