In school, we learn how a line has an equation… and a circle has an equation… what does this mean?
The short answer is
points
on curve
solutions
of equation
however this note explains all of this from first principles, with a particular emphasis on the set-theoretic fundamentals.
Set Theory
A set is a collection of objects. The objects of a set are referred to as the elements or members and if we can list the elements we include them in curly-brackets. For example, call by the set of whole numbers (strictly) between two and nine. This set is denoted by
.
We indicate that an object is an element of a set
by writing
, said,
in
or
is an element of
. We use the symbol
to indicate non-membership. For example,
.
Elements are not duplicated and the order doesn’t matter. For example:
.
The cardinality of a set is a measure of the size of the set and for finite sets is just given by the number of elements. For example, the cardinality of is equal to six. The cardinality of a set
is denoted by
and so we have
.
Things are far more complicated for infinite sets. Consider the set of natural numbers:
,
where the dots signify that there are infinitely many such numbers. It is reasonable to write something like:
,
however this turns out to give problems when we consider the cardinality of the rational numbers, , and the cardinality of the real numbers,
.
Subsets
A subset of a set , is another set
such that whenever
then
also. When this is the case, we write
. For example, the set
of odd numbers (strictly) between two and nine is a subset of the set of numbers (strictly) between two and nine:
.
Note that a set is always a subset of itself,
, because whenever
of course
.
A convenient way to think of a subset of a set is as a choice of elements from
. A subset of
is formed by making a choice for each of the elements of
whether to include them or not. For example, for the set
, the subset
is formed by making the choices:
.
Under this view, we have, for all sets, , the subset
being formed by choosing all of the elements of
.
The subset formed when we choose none of the elements of is called the empty set. Denoted by
or
, the empty set is a subset of every set:
.
How many subsets does a finite set have? Recall always that the full choice and empty choice are always subsets. Also if we collect the subsets of a set as objects we form a set: the set of subsets of
.
Let us start with the empty set, . In this case the full and empty choices coincide — as the empty set itself. There are no other choices as there are no elements to choose and so there is only one subset of
:
set of subsets of .
Also, .
Consider now the set containing one element, say . Now we can either include or not include
, giving two subsets:
set of subsets of .
We are already weary of writing “set of subsets of” so we introduce the notation :
.
So (so
, and (recalling
)
, so
.
Now consider . We have two choices for
: include or not; and two choices for
: include or not. We list:
.
Note .
We can keep listing all day, for example with three elements we have the empty set (choose none), singletons (sets with one element: choose one), two element subsets (choose two) and the full subset (choose all):
,
and so .
There is a fairly simple relationship between the cardinality of a set (denoted
), and the cardinality of the set of subsets of
,
(denoted
).
If is finite, then the cardinality of
,
is simply the number of elements in
while the cardinality of
,
, is therefore the number of subsets of
.
Proposition
For any set
,
.
Proof using Fundamental Principle of Counting: Let so that
. A subset
of
corresponds to a series of choices:
?,
?,…
?
This is tasks and there are two ways of completing each task. By the fundamental principle of counting, there are
ways of choosing a subset of
Proof by Induction: Let be the proposition that
.
Consider so that
,
.
Now assume : a set of cardinality
has
subsets. Consider
. Let
. Consider the set
. This set has a cardinality of
and so by assumption has
subsets.
Now consider again the subsets of . A subset of
is a choice of elements from
. We can form subsets of
by taking subsets of
and either including
or not. Where
is an enumeration of
, and
is the set containing all the elements of
as well as the element
, the subsets of
are given by:
,
therefore is true and so by the principle of induction
is true for all
It is because of this result that we sometimes call the power set of
(even if
is infinite).
Of course, if , and
, then
. Why? Well if
is a choice of elements of
, and
and choice of elements of
, then
is a choice of elements of
. This means that the relationship
is transitive.
It is also the case that if ,
, that
. A subset of
is a selection of some of the subsets of
. Select the subsets of
that contain only elements of
. Subsets of
(elements of
) that contain only elements of
are nothing but selections from
, i.e. subsets of
, in other words elements of
.
As an example, consider the set of real numbers, . This is all numbers that can be expressed as a decimal. We can represent it graphically using a number line:

It has positive and negative directions, a notional centre (0), and a distance corresponding to one. We can’t list all the real numbers. If we choose some real numbers we get subsets. For example, if we just choose the fractions,
,
we have a subset:
.
It isn’t immediately obvious that there are decimals that cannot be written as a fraction, elements of (elements in
but not in
— decimals that are not fractions), but it turns out there are many:
, and
…
No, , that is only an approximation. For a proof that
is not equal to any fraction see here.
Note that so we can say that:
.
Now, from the set of fractions, choose just the whole numbers (positive, negative, and zero). Note whole numbers are fractions, for example, . As the set of whole numbers,
, is a selection from
, we have
.
Also, as , we also have that
, so that
.
Similarly we have, where , is the natural numbers
,
so we can say things like
,
and indeed taking those sets as choices of elements of , we can form a subset of
. Also including the empty set (choose none of the real numbers), and
(choose all of the real numbers), and we can say things like:
.
Cartesian Products
Given two sets and
, we can form their Cartesian product
. This is a set, whose elements are ordered pairs. Pairs, because they consist of two elements: one from
and one from
, and ordered because we list the element of
first and then the element of
. For example, where
, and
,
.
We use the round brackets to emphasise that we have an ordered pair. The ordered pair is not the same as the set
because
but
is not the same as
— order matters.
The Cartesian product is the set of all such ordered pairs:
.
This is spoken, times
is defined as the set of ordered pairs
, such that
is an element of
and
is an element of
.
For example, if and
, then
.
Exercises
- Prove that for
and
,
.
- Prove that for finite sets,
.
A particular cartesian product of interest is the plane, . This is formed by taking the cartesian product of
with itself:
.
It is a set of ordered pairs, therefore, such that the first element is a real number and the second is a real number:
.
This is the ordinary plane we are all familiar with. The is from a horizontal number line (first copy of
), and the
from a vertical number line (second copy of
). Each point corresponds to some pair
, and each ordered pair
corresponds to some point on the plane (in the obvious way):
Relations
A relation between sets and
is a subset of
; that is an element of
.
For, example, where and
, any subset of
is a relation. For example,
is a relation. We have (spoken
is related to
),
, and
.
From exercise two above, this means that there are relations between finite sets
and
.
The full relation between and
is selecting all of the ordered pairs, so taking the whole of
.
The empty relation between and
is selecting none of the ordered pairs, so just the empty set
.
When we have a relation between
and itself, we just say that
is a relation on
. So a relation on
is just an element of
.
A relation on , is a subset of
, and so just a selection of points on the plane. For example, where the selected points are painted black, the following is a subset of the plane (an element of
, and so a relation on
:
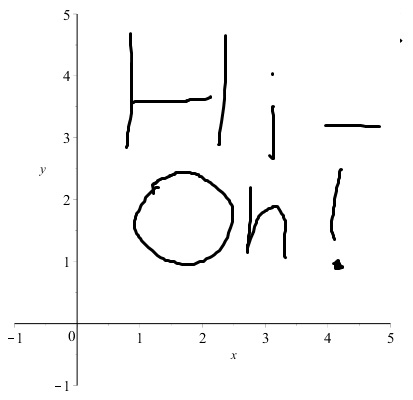
Equational Relations
Now suppose that is an equation in terms of
and
. For example,
.
Using an equation, we can define a relation on . Recall a relation on
is a subset of
, an element of
… it is a selection of ordered pairs of real numbers.
We use the equation to choose the ordered pairs and we only pick ordered pairs such that
solves the equation.
For example, the above equation defines a relation on , by only choosing the solutions:
if and only if
.
Now think of solutions as points on the plane,
. If we plot all of the solutions of the equation… in other words if we plot all elements of the relation, we have a subset of the plane.
If the equation is particularly nice, we get a nice curve. For example, the above relation, when plotted, gives:
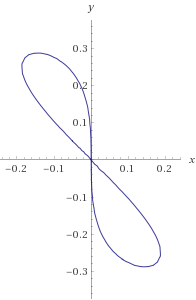
So, the answer is:
If we plot all of the solutions of an equation, we get it’s curve. This is how an equation has a curve.
This wasn’t exactly the question though was it… the question was how does a curve have an equation.
The examples of lines and circles are not that difficult. Each line has an equation whose solutions correspond precisely to the points on the curve and similarly for circles.
Do all possible curves in/subsets of the plane have such an equation? This is a much harder problem!
Exercises
- Show that
is the empty relation on
. What does the curve look like?
- Show that
is the full relation on
. What does the curve look like?

8 comments
Comments feed for this article
June 5, 2018 at 4:48 pm
On Parallel and Perpendicular Lines | J.P. McCarthy: Math Page
[…] and perpendicular are then relations on the set of lines . This gives yet another definition of a line (that does not, by the way, […]
June 5, 2018 at 4:48 pm
On Parallel and Perpendicular Lines | J.P. McCarthy: Math Page
[…] and perpendicular are then relations on the set of lines . This gives yet another definition of a line (that does not, by the way, […]
November 1, 2018 at 10:50 am
MATH6040: Winter 2018, Week 7 | J.P. McCarthy: Math Page
[…] We will look at Implicit Differentiation and Partial Differentiation. If you are interested in a very “mathsy” approach to curves you can look at this. […]
November 8, 2018 at 10:06 am
MATH6040: Winter 2018, Week 8 | J.P. McCarthy: Math Page
[…] We looked at Implicit Differentiation and Partial Differentiation. If you are interested in a very “mathsy” approach to curves you can look at this. […]
April 3, 2019 at 10:11 am
MATH6040: Spring 2019, Week 10 | J.P. McCarthy: Math Page
[…] For those who were able to make it we had some tutorial time from 18:00-19:00 for parametric, implicit, and related rates differentiation. If you are really interested in understanding how does a curve have an equation, see here. […]
October 30, 2019 at 2:02 pm
MATH6040: Winter 2019, Week 7 | J.P. McCarthy: Math Page
[…] We will finish looking at Related Rates and then look at Implicit Differentiation. If you are interested in a very “mathsy” approach to curves you can look at this. […]
March 11, 2020 at 10:05 am
MATH6040: Spring 2020, Week 7 | J.P. McCarthy: Math Page
[…] We will look at Related Rates and then look at Implicit Differentiation. If you are interested in a very “mathsy” approach to curves you can look at this. […]
March 19, 2020 at 4:22 pm
MATH6040: Spring 2020, Week 8 | J.P. McCarthy: Math Page
[…] If you are interested in a very “mathsy” approach to curves you can look at this. […]