Some notes on this paper.

1. Introduction and Main Results

A tree has no symmetry if its automorphism group is trivial. Erdos and Rényi showed that the probability that a random tree on n vertices has no symmetry goes to zero as n\rightarrow \infty.

Banica (after Bichon) wrote down with clarity the quantum automorphism group of a graph. It contains the usual automorphism group. When it is larger, the graph is said to have quantum symmetry.

Lupini, Mancinska, and Roberson show that almost all graphs are quantum antisymmetric. I am fairly sure this means that almost all graphs have no quantum symmetry, and furthermore for almost all (as n\rightarrow \infty) graphs the automorphism group is trivial.

The paper in question hopes to show that almost all trees have quantum symmetry — but at this point I am not sure if this is saying that the quantum automorphism group is larger than the classical.

2. Preliminaries

2.1 Graphs and Trees

Standard definitions. No multi-edges. Undirected if the edge relation is symmetric. As it is dealing with trees, this paper is concerned with undirected graphs without loops, and identify V=\{v_1,\dots,v_n\}\cong \{1,2,\dots,n\}. A path is a sequence of edges. We will not see cycles if we are discussing trees. Neither will we talk about disconnected graphs: a tree is a connected graph without cycles (this throws out loops actually.

The adjacency matrix of a graph is a matrix A=(a_{ik})_{i,j\in V} with a_{ij}=1 iff there is an edge connected i and j. The adjacency matrix is symmetric.

2.2 Symmetries of Graphs

An automorphism of a graph \Gamma is a permutation of V that preserves adjacency and non-adjacency. The set of all such automorphisms, \text{Aut }\Gamma, is a group where the group law is composition. It is a subgroup of S_n, and S_n itself can be embedded as permutation matrices in M_n(\mathbb{C}). We then have

\text{Aut }\Gamma=\{\sigma\in S_n\,:\,\sigma A=A\sigma\}\subseteq S_n.

If \text{Aut }\Gamma=\{e\}, it is asymmetric. Otherwise it is or rather has symmetry.

2.3 Compact Matrix Quantum Groups

A compact matrix quantum group is a pair (C(G),u), where C(G) is a unital \mathrm{C}^\ast-algebra, and u=(u_{ij})_{i,j=1}^n\in M_n(C(G)) is such that:

  • C(G) is generated by the u_{ij},
  • There exists a morphism \Delta:C(G)\rightarrow C(G)\otimes C(G), such that \Delta(u_{ij})=\sum_{k=1}^n u_{ik}\otimes u_{kj}
  • u and u^T are invertible (Timmermann only asks that \overline{u}=(u_{ij}^\ast) be invertible)

The classic example (indeed commutative examples all take this form) is a compact matrix group G\subseteq U_n(\mathbb{C}) and u_{ij}:G\rightarrow \mathbb{C} the coordinates of G.

Example 2.3

The algebra of continuous functions on the quantum permutation group S_n^+ is generated by n^2 projections u_{ij} such that the row sums and column sums of u=(u_{ij}) both equal \mathbf{1}_{S_n^+}.

The map \varphi:C(S_{n}^+)\rightarrow C(S_n), u_{ij}\mapsto \mathbf{1}_{\{\sigma\in S_n\,|\,\sigma(j)=i\}} is a surjective morphism that is an isomorphism for n=1,2,3, so that the sets \{1\},\,\{1,2\},\,\{1,2,3\} have no quantum symmetries.

2.4 Quantum Symmetries of Graphs

Definition 2.4 (Banica after Bichon)

Let \Gamma=(V,E) be a graph on n vertices without multiple edges not loops, and let A be its adjacency matrix. The quantum automorphism group \text{QAut }\Gamma is defined as the compact matrix group with \mathrm{C}^\ast-algebra:

\displaystyle C(\text{QAut }\Gamma)=C(S_n^+)/\langle uA=Au\rangle

For me, not the authors, this requires some work. Banica says that \langle uA=Au\rangle is a Hopf ideal.

A Hopf ideal is a closed *-ideal I\subset C(G) such that

\Delta(I)\subset C(G)\otimes I+I\otimes C(G).

Classically, I the set of functions vanishing on a distinguished subgroup. The quotient map is f\mapsto f+I, and f+I=g+I if their difference is in I, that is if they agree on the subgroup.

The classical version of Au=uA ends up as a_{ij}=a_{\sigma(i)\sigma(j)}… the group in question the classical \text{Aut }\Gamma. In that sense perhaps Au=uA might be better given as fA=Af.

Easiest thing first, is it a *-ideal? Well, take the adjoint of fA=Af\Rightarrow A^*f^*=f^*A^* and A=A^* so I is *closed. Suppose f\in I and g\in C(S_n^+)… I cannot prove that this is an ideal! But time to move on.

3. The Existence of Two Cherries

In this section the authors will show that almost all trees have two cherries. Definition 3.4 says with clarity what a cherry is, here I use an image [credit: www-math.ucdenver.edu]:

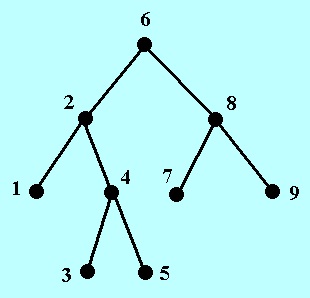
cherry

(3,5,4) and (7,9,8) are cherries

Remark 3.2

If a graph admits a cherry (u_1,u_2,v), the transposition (u_1\quad u_2) is a non-trivial automorphism.

Theorem 3.3 (Erdos, Réyni)

Almost all trees contains at least one cherry in the sense that

\displaystyle \lim_{n\rightarrow \infty}\mathbb{P}[C_n\geq 1]=1,

where C_n is #cherries in a (uniformly chosen) random tree on n vertices.

Corollary 4.3

Almost all trees have symmetry. 

The paper claims in fact that almost all trees have at least two cherries. This will allow some S_4^+ action to take place. This can be seen in this paper which is the next point of interest.