Consider the symmetric group S_N. Let \mathrm{fix}_N \in C(S_N) count the number of fixed points of a permutation \sigma\in S_N. Where X\sim \mathrm{Poi}[1], we have that for a random permutation \xi_N\in S_N chosen with respect to the uniform distribution, the \mathrm{fix}_N converges in distribution to X in the sense that:

\displaystyle \lim_{N\to \infty}\mathbb{P}[\mathrm{fix}_N(\xi_N)=m]=\mathbb{P}[X=m].

In this note we will look at the distribution in the case where the uniform distribution is conditioned on \xi_N(1)=1.

Theorem

Let \xi_N\in S_N be chosen according to the distribution uniform on permutations for which one is a fixed point. The number of fixed points has distribution 1+\mathrm{Poi}[1] in the sense that, where X\sim \mathrm{Poi}[1],

\displaystyle \lim_{N\to \infty}\mathbb{P}[\mathrm{fix}_N(\xi_N)=m]=\mathbb{P}[X=m-1].

Proof: What can be shown, ostensibly from stuff from the quantum permutation side of the house is that, where h_N is integration against the uniform distribution, and \widetilde{h_N} is integration against the uniform distribution on permutations with one a fixed point, that, for k<N:

\displaystyle \widetilde{h_N}(\mathrm{fix}_N^k)=h_N(\mathrm{fix}_N^{k+1})=B_{k+1},

the (k+1)-st Bell number. Now consider the moments of 1+X:

\displaystyle \sum_{t=0}^\infty t^k\mathbb{P}[1+X=t]=\sum_{t=0}^\infty t^k\mathbb{P}[X=t-1]

\displaystyle =\sum_{t=1}^\infty t^k\frac{e^{-1}}{(t-1)!}

\displaystyle \underset{s=t-1}{=}\sum_{s=0}^\infty(s+1)^k\frac{e^{-1}}{s!}

\displaystyle =\sum_{s=0}^\infty\sum_{i=0}^k\binom{k}{i}s^i \frac{e^{-1}}{s!}

\displaystyle =\sum_{i=0}^k\binom{k}{i}\sum_{s=0}^\infty s^i\frac{e^{-1}}{s!}

\displaystyle =\sum_{i=0}^k \binom{k}{i} B_k=B_{k+1},

using the fact that the Bell numbers are the moments of that Poisson distribution and the standard recurrence for the Bell numbers.

Local vs Global Conditioning of Quantum Permutations

In the quantum case we define

\displaystyle \mathrm{fix}_N:=\mathrm{Tr}(u),

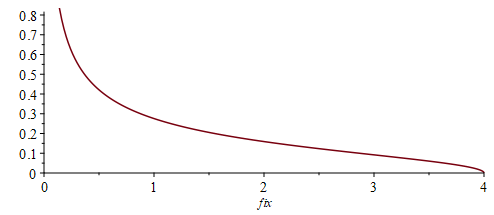
where u\in M_N(C(S_N^+)) is the fundamental magic representation. The moments of \mathrm{fix}_N with respect to the Haar state are the Catalan numbers and it follows that the law of \mathrm{fix}_N is a Marchenko-Pastur distribution, with density

\displaystyle \dfrac{1}{2\pi}\sqrt{\frac{4}{t}-1}:

Note that when we measure the Haar state with some finite spectrum version of \mathrm{fix}_N we find:

  • the probability of finding an integer number of fixed points is zero, and
  • independently of N, the probability of finding more than four fixed points is zero.

In the classical case above when we chose the permutation uniformly from those who fix one, there are two ways of viewing it:

  • we pick an element of S_N that fixes one, OR
  • we consider the isotropy subgroup S_{N-1}\subset S_N and choose our permutation from S_{N-1}.

Classically, these are the same thing. In the quantum case these two things can be interpreted differently. The second case is quite clear in the quantum case. For N>4, we take the isotropy S_{N-1}^+\subset S_N^+ via the quotient C(S_N^+)\to C(S_N^+)/\langle1-u_{11}\rangle.

The analogue of the uniform distribution on S_{N-1}\subset S_N here is the Haar idempotent h_{C(S_{N-1}^+)}\circ \pi. Note this maps \mathrm{fix}_N to 1+\mathrm{fix}_{N-1}. Now, using the fact that h_{C(S_{N-1}^+)}(\mathrm{fix}_{N-1})=C_k, the Catalan number, we have that the moments of \mathrm{fix}_N with respect to h_{C(S_{N-1}^+)}\circ \pi is the binomial transform of the Catalan numbers (the binomial transform of B_1,\dots,B_k is B_{k+1}). It follows, using similar stuff to the above, that the distribution of \mathrm{fix}_N with respect to h_{C(S_{N-1}^+)}\circ \pi is just a shifted version of Marchenko–Pastur:

I guess this is marginally more interesting than the unshifted version.

Now, what about an analogue of “we pick an element of S_N that fixes one”. So if we take the Haar state and measure the observable u_{11}\in C(S_N^+) that asks of a quantum permutation, does it fix one, we get, conditioned on this, the state:

\displaystyle h_1(f):=N\cdot h(u_{11}fh_{11})=\dfrac{h(u_{11}fu_{11})}{h(u_{11})}\qquad (f\in C(S_N^+)).

And, it turns out, as above, using stuff from the quantum permutation side of the house:

\displaystyle h_1(\mathrm{fix}_N^k)=h(\mathrm{fix}_N^{k+1})=C_{k+1}.

Quite quickly from here we find that the density of the distribution of \mathrm{fix}_N with respect to h_1 is

\displaystyle \frac{t}{2\pi}\sqrt{\frac{4}{t}-1}

This is so interesting:

  • it doesn’t change the support — we still find between 0 and 4 fixed points,
  • we have a new symmetry about \mathrm{fix}_N=2, we had another unexpected symmetry here.
  • the mean jumps from one to two, that is not unexpected, but
  • the mode jumps from zero to two!
  • even though we have observed one to one, there can still be less than one fixed point when we measure… and this happens with probability \approx 1/5.

The next obvious question is what happens with:

\displaystyle f\mapsto \dfrac{h_1(u_{22}fu_{22})}{h_1(u_{22})}\qquad (f\in C(S_N^+))

Epilogue?

So what about this local vs global conditioning? Well, no matter what subsequent measurements are made to h_{C(S_{N-1}^+)}\circ \pi, we will always find that one is a fixed point. That conditioning is ‘global’.

This is not the case with h_1, and why the support of the law is not bounded above one, like that of the globally conditioned h_{C(S_{N-1}^+)}\circ \pi. In fact, there is a non-zero probability that h_1 is observed to fix two but then subsequently not fix one anymore. That conditioning was only local: the probability that h_1 fixes one is 100%… but subsequent measurements can destroy that conditioning… it is only local.