At Leaving Cert you are only required to prove the Factor Theorem for cubics. This is a more general proof.
The Factor Theorem is an important theorem in the factorisation of polynomials. When is a factor of a polynomial
then
for some polynomial
and clearly
is a root. In fact the converse is also true. Most proofs rely on the division algorithm and the remainder theorem; here a proof using strong induction on the degree of the polynomial is used. See Hungerford, T.W., (1997), Abstract Algebra: An Introduction. Brooks-Cole: U.S.A for the standard proof (this reference also describes strong induction).
Factor Theorem
is a root of a polynomial
if and only if
is a factor:
where
is a polynomial.
Proof:
Suppose deg . Then
and
. Clearly
and
is a polynomial (of degree 0).
Suppose for all polynomials of degree less than or equal to , that
a root implies
a factor. Let
be a polynomial of degree
and assume
a root. Now
Now each for
is a polynomial of degree less than or equal to
, with a root
, hence
is a factor of each. Thence
where
is a polynomial:
Now but
is a polynomial of degree
with root
and hence
is a factor:
Hence
Hence a factor

2 comments
Comments feed for this article
January 13, 2012 at 12:00 am
Keith Burke
Thanks for this. I am not sure my sixth years would follow this. It’s quite involved.
January 13, 2012 at 9:18 am
J.P. McCarthy
Keith,
Yes I appreciate this — however I didn’t think LC students would offer this proof on an exam.
In my opinion, this proof is easier than the standard proof (of the general theorem — not just the LC version for cubics).
It is important that the students know that the factor theorem is true for more than just cubics though. In the new Paper 1 syllabus the proof of the factor theorem (for cubics) is not examinable, although the application of the more general theorem is (i.e. for looking at polynomials of degree larger than 3) is.
It also invoked implicitly for DeMoivre’s Theorem. A proof of the Fundamental Theorem of Algebra (a polynomial of degree has
has  roots) uses the factor theorem. Thus if you are solving the equation
roots) uses the factor theorem. Thus if you are solving the equation  (i.e. finding
(i.e. finding  th roots of
th roots of 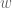 ), you know there are
), you know there are  answers (
answers ( roots).
roots).
Regards,
J.P.