I am emailing a link of this to everyone on the class list every Wednesday morning. If you are not receiving these emails or want to have them sent to another email address feel free to email me at jippo@campus.ie and I will add you to the mailing list.
This Week
In lectures, we finished off chapter 2.
In tutorials we did p.17 Q.1 (d)(f), p.32 Q.1,9, p.36 Q. 7, 8, 12 and p.39 Q. 2, 3.
Teaching Practise
Be aware that these two weeks are a terrible risk to you falling behind in integration so make serious efforts to either keep up with the work or catch up ASAP: week 4’s lectures.
Note that I will not be scanning up any more of these notes.

2 comments
Comments feed for this article
May 3, 2012 at 10:06 am
Student 13
In our notes on page 43 for the autumn exam question why do u let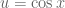 when the integral can be broken up into
when the integral can be broken up into 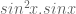 and so could use
and so could use  as
as  ?
?
May 3, 2012 at 10:16 am
J.P. McCarthy
The start of section 2.4 explains why choosing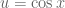 should work. However, we can talk more generally and say that the whole time when doing substitutions we are looking for the function-(multiple of-)derivative pattern. We have it here:
should work. However, we can talk more generally and say that the whole time when doing substitutions we are looking for the function-(multiple of-)derivative pattern. We have it here:
So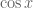 is a function (inside another which is fine), and
is a function (inside another which is fine), and  is a multiple of its derivative.
is a multiple of its derivative.
You could do your substitution but it’s a lot longer and harder:
The best we can do with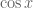 is
is  so we get
so we get
This needs a substitution of the form to get
to get
It takes a little work to see that this equals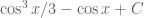 .
.