MATH6037: Spring 2017, Week 3

I am emailing a link of this to everyone on the class list every week. If you are not receiving these emails or want to have them sent to another email address feel free to email me at jpmccarthymaths@gmail.com and I will add you to the mailing list.

Quiz 2 Results

Below find the results. You are identified by the last four digits of your student number unless you are excelling. The marks are out of 2.5 percentage points. Your best eight quizzes go to the 20% mark for quizzes. The R % column is your running percentage (for best eight quizzes). The QPP is your Quiz Percentage Points. MPP is your Maple percentage points. GPP is your gross percentage points. One student didn’t write down their name for Quiz 1. They should email me.

S/N	Q1	Q2	R%	QPP	MPP	GPP
Fahey	2.5	2.5	100	5	1.5	6.5
Nolan	2.43	2.5	98.6	4.93	1.5	6.43
B Murphy	2.37	2.5	97.4	4.87	1.5	6.37
8426	2.24	2.5	94.8	4.74	1.5	6.24
9464	2.17	2.5	93.4	4.67	1.5	6.17
6645	2.17	2.5	93.4	4.67	1.5	6.17
1486	2.24	2.4	92.8	4.64	1.5	6.14
2327	2.5	1.72	84.4	4.22	1.5	5.72
7879	1.12	2.5	72.4	3.62	1.5	5.12
8332	2.37	1.22	71.8	3.59	1.5	5.09
2073	0.99	2.5	69.8	3.49	1.5	4.99
2942	1.71	1.7	68.2	3.41	1.5	4.91
3703	1.71	1.2	58.2	2.91	1.5	4.41
2128	2.24	0.4	52.8	2.64	1.5	4.14
3481	1.71	0.3	40.2	2.01	1.5	3.51
9896	1.97	0	39.4	1.97	0	1.97
1298	0	1.9	38	1.9	0	1.9
1321	1.45	0.4	37	1.85	1.5	3.35
2237	1.71	0	34.2	1.71	1.5	3.21
2257	0.53	0.6	22.6	1.13	1.5	2.63
9555	0.53	0	10.6	0.53	0	0.53
9951	0.53	0	10.6	0.53	0	0.53
2070	0.33	0.2	10.6	0.53	1.5	2.03
8425	0	0.4	8	0.4	1.5	1.9
7209	0.39	0	7.8	0.39	0	0.39
8354	0.39	0	7.8	0.39	1.5	1.89
3872	0.26	0	5.2	0.26	1.5	1.76
4402	0	0	0	0	0	0
2092	0	0	0	0	0	0

Quiz 3 Question Bank

Question bank for Quiz 3 (in Week 4) is as follows:

P. 35, Q.1-4, 7,8, 10 (yes, again)
P. 50, Q. 1 (i) and (ii)

If you have any specific difficulties with these questions, please email me. Alternatively use Maple or Wolfram Alpha to help. Your Quiz 3 Questions will be taken from these. The final answers will not be given on the quiz paper and neither is there any value in writing down the final answers alone — you will receive marks for full and correct solutions — but nothing for final answers without justification or skipping important steps. No hints will appear either. Please don’t learn off model solutions — you need to understand the material not just on a superficial level to do well later on.

Quiz 3 runs from 19:00 to 19:15 sharp on Wednesday 22 February.

Maple Labs

The next Maple Lab is 1 March.

Week 3

We started Partial Differentiation which we will eventually use to do Error Analysis.

In Maple we did some basic plotting, differentiation and integration.

Week 4

We will finish off Chapter 1.

Plan

Week 3: Maple Lab 1 & Section 1.4
Week 4: Section 1.4 & Section 1.5
Week 5: Maple Lab 2 & Section 2.1
Week 6: Section 2.2 & Sections 3.1-3.3
Week 7: Maple Lab 3 & Sections 3.1-3.3
Week 8: Maple Lab 4 & Section 3.4
Week 9: Section 3.4
Week 10: Maple Lab 5 & Section 3.4
————-EASTER————–
Week 11: Maple Test & Section 3.4
Week 12: Section 3.5
————-END OF LECTURES———-
Week 13: Review Class — Summer 2015 Paper

Academic Learning Centre

I would urge anyone having any problems with the material to use the Academic Learning Centre. You will get best results if you come to the helpers there with specific questions.

Study

Please feel free to ask me questions about the exercises via email or even better on this webpage. Anyone can give me exercises they have done and I will correct them. I also advise that you visit the Academic Learning Centre.

Student Resources

Please see the Student Resources tab on the top of this page for information on the Academic Learning Centre, etc..

11 comments

Comments feed for this article

February 16, 2017 at 9:04 pm

Michael Ferriter

Hey jp.

Can I mail you pics of some of the problems I’m having.

Thanks

February 16, 2017 at 9:12 pm

J.P. McCarthy

Michael,

No problem.

Email away… I should get back to you tomorrow.

Regards,
J.P.

February 18, 2017 at 4:47 pm

michael

In Q.8 P.35 how does ∫ tan⁡θ.dθ get to log|secθ|

February 19, 2017 at 1:23 pm

Sean O'Reilly

Mick the anti-derivitive of tan⁡θ is log|secθ|. It’s not in the tables so it’s something you will need to know. The anti-derivitive of dθ is 1 so you just lose that and your left with log|secθ|. That’s my understanding of it anyway.

February 19, 2017 at 1:32 pm

My bad Mick it is in the tables!!

February 20, 2017 at 1:24 pm

Sean is correct but not when he says that the antiderivative of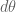 $d\theta$ is one. The anti-derivative of 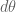$d\theta$ doesn’t really make sense but we do have

$\displaystyle \int d\theta=\theta+C$ .

This isn’t even saying that the anti-derivative of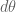 $d\theta$ is $\theta$ but in fact:

$\displaystyle \int d\theta=\int 1\cdot d\theta=\theta+C,$

i.e. the anti-derivative of $1$ with respect to $\theta$ is $\theta$ … as:

$\displaystyle \frac{d}{d\theta}\theta=1$ .

See https://jpmccarthymaths.com/2017/02/09/math6037-spring-2017-week-2/#comment-5857 to understand the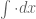 $\int \cdot dx$ notation better…

Regarding the anti-derivative of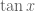 $\tan x$ … OK step one says look in the tables and it is the tables…

$\displaystyle \int \tan \theta\,d\theta=\ln(\sec\theta)+C$ …

Suppose it wasn’t in the tables… we would have to try a manipulation…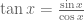 $\tan x=\frac{\sin x}{\cos x}$ so we have:

$\displaystyle \int \frac{\sin \theta}{\cos\theta}\,d\theta$ .

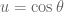Now I don’t know of any other useful manipulations… and we have no quotient rule so I could try a substitution. For two reasons (it is ‘inside’ the ‘one-over’ and also its derivative $-\sin \theta$ is a multiple of $\sin\theta$ ) I pick $u=\cos \theta$ . This gives

$\displaystyle \frac{du}{d\theta}=-\sin \theta\Rightarrow d\theta=-\frac{du}{\sin \theta}$ :

$\displaystyle \int \frac{\sin \theta}{\cos\theta}\,d\theta=\int \frac{\sin \theta}{u}\cdot\left(- \frac{du}{\sin\theta}\right)$

$\displaystyle =-\int \frac{1}{u}\,du=-\ln|u|=-\ln|\cos \theta|$ .

Now we use the following property of logs that they turn powers into multiplication:

$\displaystyle \log(x^n)=n\cdot \log (x)$ to write

$\displaystyle -\ln|\cos \theta|=-1\cdot \ln|\cos \theta|=\ln |\cos \theta|^{-1}$

$\displaystyle =\ln \left(\frac{1}{|\cos \theta|}\right)=\ln \left|\frac{1}{\cos \theta}\right|=\ln|\sec\theta|+C$ ,

by the definition of $\sec x$ .

As you can see, it is a good idea that we put it in the tables!!

February 18, 2017 at 5:44 pm

Hi J.P,
Do you have a link where we could download maple Please?

Cheers,
Sean

February 19, 2017 at 10:22 am

Sean,

Go to the webpage and go to the Student Resources tab.

The relevant information is in there.

February 19, 2017 at 1:25 pm

Cheers JP

February 20, 2017 at 1:07 pm

Student

For Q.1 (ii) when differentiating $x^2e^y - 4y$ wr t $y$ , when $y$ is the power does it remain as $y$ because looking at the solution it remains as $x^2e^y$ .

Regards.

February 20, 2017 at 1:10 pm

OK, using the linear property of differentiation, we can differentiate term-by-term and pull out constants. Recall that with respect to $y$ that $x^2$ is a constant:

$\displaystyle \frac{\partial}{\partial y}\left(x^2e^y-4y\right)=x^2\frac{\partial}{\partial y}e^y-4\frac{\partial}{\partial y}y$ .

Now the exponential function is defined as the function which is A) equal to its own derivative and B) equal to one at zero. Therefore the exponential function is its own derivative so we have:

$\displaystyle x^2\frac{\partial}{\partial y}e^y-4\frac{\partial}{\partial y}y=x^2e^y-4(1)=x^2e^y-4$ .

	J.P. McCarthy on MATH6040: Spring 2022, Week…
	J.P. McCarthy on MATH6040: Spring 2022, Week…
	J.P. McCarthy on MATH7019: Winter 2020, Week…
	J.P. McCarthy on MATH7019: Winter 2020, Week…
	A Sufficient Conditi… on Almost All Trees have Quantum…

MATH6037: Spring 2017, Week 3

Quiz 2 Results

Quiz 3 Question Bank

Maple Labs

Week 3

Week 4

Plan

Academic Learning Centre

Study

Student Resources

Recent Comments

Categories

J.P. McCarthy Maths

11 comments

Leave a Reply to J.P. McCarthy Cancel reply

MATH6037: Spring 2017, Week 3

Quiz 2 Results

Quiz 3 Question Bank

Maple Labs

Week 3

Week 4

Plan

Academic Learning Centre

Study

Student Resources

Share this:

Like this:

Related

Recent Comments

Categories

J.P. McCarthy Maths

11 comments

Leave a Reply to J.P. McCarthy Cancel reply