Quiz 8 Results
Below find the results. Your best eight quizzes go to the 20% mark for quizzes. The R % column is your running percentage (for best eight quizzes). The QPP is your Quiz Percentage Points (a max of 25 at the moment). MPP is your Maple percentage points. GPP is your gross percentage points.
| S/N | Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Q7 | Q8 | R% | QPP | MPP | GPP/25 |
| 1298 | 1.6 | 1.2 | 1.6 | 49.5 | 9.9 | 5.63 | 15.53 | |||||
| 2327 | 1.4 | 1 | 2.2 | 72.1 | 14.42 | 7.50 | 21.92 | |||||
| 2073 | 2.5 | 2.5 | 2.5 | 92.5 | 18.49 | 7.50 | 25.99 | |||||
| 8332 | 2.5 | 2.5 | 0.8 | 72.0 | 14.39 | 7.50 | 21.89 | |||||
| 9464 | 2.5 | 0 | 2.5 | 80.4 | 16.07 | 7.50 | 23.57 | |||||
| 3872 | 1.4 | 0 | 0 | 26.8 | 5.36 | 5.63 | 10.99 | |||||
| 1480 | 2.3 | 2.5 | 2.5 | 91.9 | 18.37 | 7.50 | 25.87 | |||||
| 2237 | 1.4 | 1.6 | 0.9 | 39.0 | 7.79 | 7.50 | 15.29 | |||||
| 2070 | 2.5 | 2.5 | 2.2 | 73.0 | 14.6 | 7.50 | 22.10 | |||||
| 3481 | 2.3 | 2.5 | 2.1 | 69.3 | 13.85 | 7.50 | 21.35 | |||||
| 3703 | 2.5 | 0.3 | 2.5 | 68.8 | 13.76 | 7.50 | 21.26 | |||||
| 7879 | 2.4 | 2.5 | 2.2 | 72.1 | 14.42 | 7.50 | 21.92 | |||||
| 2257 | 1.8 | 1.3 | 1.9 | 53.4 | 10.67 | 7.50 | 18.17 | |||||
| 8425 | 2.4 | 1.3 | 1.5 | 50.2 | 10.03 | 7.50 | 17.53 | |||||
| 9896 | 0 | 0 | 0 | 9.9 | 1.97 | 0.00 | 1.97 | |||||
| 8212 | 2.5 | 1.5 | 2.5 | 92.2 | 18.44 | 7.50 | 25.94 | |||||
| 1486 | 0 | 0 | 0 | 35.7 | 7.14 | 1.88 | 9.02 | |||||
| 5484 | 2.5 | 2.5 | 0 | 76.7 | 15.33 | 7.50 | 22.83 | |||||
| 1321 | 1.9 | 1.5 | 2 | 51.2 | 10.23 | 7.50 | 17.73 | |||||
| 2128 | 1.5 | 1.6 | 0.6 | 67.1 | 13.42 | 7.50 | 20.92 | |||||
| 2942 | 2.5 | 1.4 | 1 | 68.3 | 13.65 | 7.50 | 21.15 | |||||
| 6645 | 2.5 | 2.5 | 1.9 | 95.4 | 19.07 | 7.50 | 26.57 | |||||
| 8426 | 2.5 | 2.5 | 2.5 | 67.2 | 13.44 | 5.63 | 19.07 | |||||
| 2092 | 1.6 | 1 | 0 | 14.0 | 2.8 | 5.63 | 8.43 | |||||
| 8354 | 1.9 | 0.5 | 0 | 24.6 | 4.91 | 7.50 | 12.41 |
Maple Test
The 2.5% Maple Test will take place in Week 12. You will receive a sample Maple Test in good time.
Quiz 9
You have three weeks to prepare for this quiz. The 2.5% available isn’t really that important but the bulk of your learning for Laplace Transforms will be done by doing these exercises. Do not hesitate to contact me via email over the Easter break.
P. 123,
- Q. 1,
- Q. 2 i., ii. but not iii.
- Q. 3 (b), (c) but not (a)
P. 124,
- Q. 7 all but not ix. For answers use Maple or Wolfram Alpha.
P. 125
- Q. 8 (a) – (c), (e), (j)
Quiz 9 runs from 19:00 to 19:15 sharp on Wednesday 26 April.
Week 10
We spoke about Inverse Laplace Transforms including the topic of Partial Fractions. We didn’t quite finish Inverse Laplace Example 4.
Week 11
Hopefully we will finish talking about Inverse Laplace Transforms and see the application of Laplace Transforms to Differential Equations.
Week 12
We will finish our studies with the case study of a damped harmonic oscillator; e.g. a door closer. Also a Maple Test and a quiz.
Week 13
Review Class — Summer 2015 Paper. The 11th quiz will be in Week 13.
Maple Catch Up
If you want to do Maple catch up (if you miss a lab) you have two options:
- download the Maple file from your email, do the exercises in Maple (either in a new worksheet or on top of the original file with the exercises), save the worksheet and email me the worksheet you were working on.
- come in for a double Maple session on a ‘Maple’ night.
Academic Learning Centre
I would urge anyone having any problems with the material to use the Academic Learning Centre. You will get best results if you come to the helpers there with specific questions.
Study
Please feel free to ask me questions about the exercises via email or even better on this webpage. Anyone can give me exercises they have done and I will correct them. I also advise that you visit the Academic Learning Centre.
Student Resources
Please see the Student Resources tab on the top of this page for information on the Academic Learning Centre, etc..

8 comments
Comments feed for this article
April 9, 2017 at 4:49 pm
Sean O'Reilly
Hi J.P. Would it be possible to get some workings for the Q1 Part I II & III. I’ve just spent the last hour and a half trying to make a start on this and I can’t get my head around it.
Cheers,
Sean
April 10, 2017 at 12:36 pm
J.P. McCarthy
Sean,
i. we are good with sums so multiply out the top, then divide each term by and then send back using the tables.
and then send back using the tables.
ii. Look in the tables. This looks like
except for those fours… try dividing above an below by four.
iii. This doesn’t look like anything in the (new) tables. We need to write this as a sum of simple things which ARE in the tables. How we do this is via partial fractions. The first step is to factorise the denominator:
You end up with two Rule Is. You can use the Cover-Up Method when you have all Rule Is.
Regards,
J.P.
May 8, 2017 at 7:41 am
Student
Hi J.P.,
Just doing a bit of revision on a question we did in our notes: I am wondering (where I have circled in green) why is there a minus? Why did the have to go to the right hand side?
have to go to the right hand side?
Regards.
May 8, 2017 at 7:45 am
J.P. McCarthy
First of all it should be
First ensure you understand that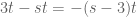 .
.
Secondly I want it in this form because I want it to look like
(with because I know that as
because I know that as  gets big
gets big 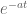 gets small.
gets small.
In this case as long as , that is
, that is  ,
, 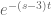 gets small for
gets small for 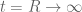 .
.
You don’t HAVE to do this messing around. If you want arrive at
and just say as long as you have a negative exponential, such that for
you have a negative exponential, such that for  , it goes to zero.
, it goes to zero.
I hope that helps.
Regards,
J.P.
May 9, 2017 at 1:34 pm
Student
Hi J.P.
Could you just explain how you complete the square with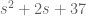 .
.
Regards.
May 9, 2017 at 1:42 pm
J.P. McCarthy
So, you have looked in the tables for what you have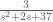 and saw nothing.
and saw nothing.
Your next thought should be “I should write this as a sum of simple terms that are in the tables… partial fractions”.
The first step in partial fractions is to factorise the bottom. This is impossible ( ) and so you look in the tables again. Your Laplace Transform looks like the transform of a sine:
) and so you look in the tables again. Your Laplace Transform looks like the transform of a sine:
but perhaps with the shifted to
shifted to 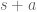 . Therefore you are thinking:
. Therefore you are thinking:
So you need to complete the square… you need to write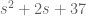 in the form
in the form  … so you force them equal to each other:
… so you force them equal to each other:
Now compare. They both have an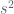 so that is grand. Next look at the
so that is grand. Next look at the  … you have
… you have  and this must match up with
and this must match up with 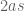 … therefore you need
… therefore you need  .
.
Solve that…
Next you need the constant on the left,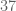 , to equal the constant on the right,
, to equal the constant on the right, 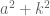 .
.
Now you know from earlier…
from earlier…  … so really you want:
… so really you want:
This gives … take
… take  .
.
So
which can be confirmed by multiplying out the RHS.
Regards,
J.P.
July 11, 2017 at 9:26 am
Student
Hi J.P.,
Just a few questions:
1. Is there any questions different from Autumn 2015, Winter 2015 or Winter 2016 that i should know about for August 2017?
2. Can you explain of give an example from you email
“You will need the differance of two squares factorisation
3. Example of a “harder” differential equation?
4. Example or answer to
“Find the Laplace Transform of a*t?”
5. Will we need to know the Midpoint, Trapezoid and Simpsons rule off by heart?
6. What’s is the formula for the Inverse Laplace Transform of
6. Any other important info I might need to know ?
Thanks for all the info and help over the last few months
Best wishes.
July 11, 2017 at 9:46 am
J.P. McCarthy
Assuming you managed to borrow a colleague’s manual…
1. I am not prepared to go any further on this point than what was said in the email of 22 June, 2017.
2. Suppose you need to find the partial fraction expansion of, say,
The first step in doing a partial fraction expansion is to factorise the bottom/denominator.
So for example here you need to factorise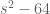 . It is a difference of two squares:
. It is a difference of two squares:
and so according to the ‘difference of two squares’ identity:
3. It is harder because it is ‘second order’ (with a second derivative) rather than ‘first order’ (with just a first derivative). Good examples might include Example 4 on p.130 and the pendulum equation at the bottom of p.151 (but with values for and
and 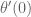 — basically there is a second derivative knocking around — the general technique isn’t any different.
— basically there is a second derivative knocking around — the general technique isn’t any different.
4. This is done at the bottom of p.91. Well this is done with . If you can do it with e.g.
. If you can do it with e.g. 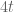 you will be rightly set up.
you will be rightly set up.
5. Versions of the Simpson’s and Trapezoidal Rules are in the examination tables. The Midpoint Rule is not and would have to be known (thankfully it is the easiest to remember).
6.
Regards,
J.P.