Test 2
Thursday 23 November at 09:00 in the usual lecture venue. You will be given a copy of these tables. Based on Chapter 3, samples at the back of Chapter 3 and also here (Q. 4 has a typo — it should be ). I strongly advise you that attending tutorials alone will not be sufficient preparation for this test and you will have to devote extra time outside classes to study aka do exercises.
Week 10
We started Chapter 4 by looking at integration by parts. We started looking at completing the square.
Week 11
We will look at completing the square and work.
Week 12
We will look at centroids and centres of gravity.
Week 13
There is an exam paper at the back of your notes — I will go through this on the board in the lecture times (in the usual venues):
- Monday 16:00
- Tuesday 09:00
- Thursday 09:00
We will also have tutorial time in the tutorial slots. You can come to as many tutorials as you like.
- Monday at 09:00 in E15
- Monday at 17:00 in B189
- Thursday at 12:00 in B180
Study
Please feel free to ask me questions about the exercises via email or even better on this webpage.
Student Resources
Please see the Student Resources tab on the top of this page for information on the Academic Learning Centre, etc.

4 comments
Comments feed for this article
November 21, 2017 at 8:22 am
Student
Hi J.P.,
Could you correct these for me please and tell me how to do Q4 aswell.
Thanks a lot.
November 21, 2017 at 8:34 am
J.P. McCarthy
Regarding Q. 1, and it is not true that
and it is not true that
If you divide above and below you by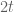 you get:
you get:
Regarding Q. 2, area doesn’t come into it at all.
Regarding Q. 3, you have the slope correct but note the question doesn’t ask for anything more.
Regarding Q. 4 you need to know that:
For Q. 5, you lose one mark for not including the unit. After that, please round the error to one significant figure (because using the differential is a rough approximation):
and match the precision (because beyond this is within margin of error: no decimal places in this case) with the calculated value:
so your answer reads
Regards,
J.P.
November 21, 2017 at 4:03 pm
Student
J.P.,
I’m one of your maths student and was wondering if you could help with the question we were doing for tutorial. It’s question 5 of the last Test 2 paper you sent us. I’ve attempted it and just wanted to see if I was right and if not if you could show or tell me where I went wrong please.
November 21, 2017 at 4:20 pm
J.P. McCarthy
The error is never going to be zero, so you have certainly gone wrong. I don’t see how you get zero or where you calculated the partial derivatives.
Solution: We have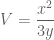 . We have measurements
. We have measurements  and
and 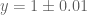 .
.
Our best guess for , which we denote by
, which we denote by  , is given by:
, is given by:
We approximate the error in this calculation, due to the error in the measurements of and
and 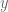 using differentials:
using differentials:
We therefore need to differentiate partially with respect to
partially with respect to  and
and 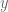 . The quickest way is to rewrite:
. The quickest way is to rewrite:
and
Alternatively, using the Quotient Rule on :
:
Therefore
Evaluating the derivatives at the measurements:
The absolute value of is
is 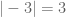 , so
, so
It is good practise to round this to one significant figure because it is a rough approximation (not applicable here) and also, with the calculation, , to match the precision: in this case two decimal places: everything beyond the second decimal place is within the margin of error.
, to match the precision: in this case two decimal places: everything beyond the second decimal place is within the margin of error.
Answer therefore,
This question is missing context that would tell us the units. If there are units they must be included.
Regards,
J.P.