Please put my name on your homework handup also
Please find the Homework. Before you open it don’t be too alarmed: you only have to do ONE of the SIX options. All of the options are about dynamical systems in different areas of math:
- Discrete Mathematics, Number Theory & Abstract Algebra
- Probability
- Differential Calculus
- Integral Calculus
- Linear Algebra
- History of Mathematics
Therefore, if you are good at differential calculus, for example, you should have a look at option 3.
All of these questions are unseen to you and all require some knowledge of modules you are doing now or have done before. Although we have been concentrating on real-valued functions on the set of real numbers (i.e. , etc.), a lot of the theory carries over into more general sets and functions, and this is the main learning outcome of this homework.
I am not going to pretend that this is an easy assignment, but I will say that clear and logical thinking will reveal that the solutions and answers aren’t ridiculously difficult: a keen understanding of the principles of dynamical systems and a good ability in one of the options should see you through.
For those who are still not happy there is an essay option.
The final date for submission is 24 April 2012 and you can hand up early if you want. You will be submitting to the big box at the School of Mathematical Science. If I were you I would aim to get it done and dusted early as this is creeping into your study time and is very close to the summer examinations.
Note that you are will be free to collaborate with each other and use references but this must be indicated on your hand-up in a declaration. Evidence of copying or plagiarism (although this is unlikely as these are original problems by and large) will result in divided marks or no marks respectively. You will not receive diminished marks for declared collaboration or referencing although I demand originality of presentation. If you have a problem interpreting any question feel free to approach me, comment on the webpage or email.
Ensure to put your name, student number, module code (MS 3011), and your declaration on your homework.

18 comments
Comments feed for this article
April 3, 2012 at 2:37 pm
Student 5
Just a quick question on the homework. I am stuck on Question 3 part (f). It says to find an expression so I have differentiated a number of times and have spotted the pattern. The problem is I am having trouble finding an expression for that pattern for
a number of times and have spotted the pattern. The problem is I am having trouble finding an expression for that pattern for  times differentiated. Just asking is there anything you can tell me to help me with this.
times differentiated. Just asking is there anything you can tell me to help me with this.
April 3, 2012 at 2:41 pm
J.P. McCarthy
I presume you have (after a product rule):
Well…
Regards,
J.P.
April 3, 2012 at 3:13 pm
Student 6
Ok so for Question 5, part i, what do you mean by seeds?
Also for part e, is there any way you could give me a hint how to start that problem?
April 3, 2012 at 3:21 pm
J.P. McCarthy
For question (e) we want to show that if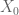 is a fixed point of
is a fixed point of 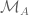 then
then 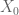 is a period 4 point of
is a period 4 point of  : that is
: that is  .
.
Hence we know that
Try and calculate .
.
Note that![\sqrt{\sqrt{A}}=\sqrt[4]{A}](https://s0.wp.com/latex.php?latex=%5Csqrt%7B%5Csqrt%7BA%7D%7D%3D%5Csqrt%5B4%5D%7BA%7D&bg=ffffff&fg=545454&s=0&c=20201002) .
.
A seed is mentioned in the general theory section on the first page. It is the zeroth iterate, or the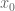 . HINT for (i): Think of inverses.
. HINT for (i): Think of inverses.
Regards,
J.P.
April 3, 2012 at 8:14 pm
Student 7
I am currently at the homework assignment and I am finding Question 1 (c) difficult. Can you give me some help on how to start it off? Must it be worked out as normal like a long division question. Thanks,
April 3, 2012 at 8:27 pm
J.P. McCarthy
Recall what we did in the tutorial where we did the question for p=1 and n=2. Our answer (with extended explanations) went something like this:
Consider solutions of or, equivalently, roots of the polynomial
or, equivalently, roots of the polynomial  . These are fixed points of
. These are fixed points of 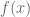 .
.
We want to show that divides into
divides into 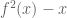 . Note that all we know about
. Note that all we know about 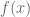 is that it is a polynomial, and although we can’t carry out an actual long division, we do use facts about the division of polynomials, namely the Factor Theorem ( http://en.wikipedia.org/wiki/Factor_theorem), which states that if
is that it is a polynomial, and although we can’t carry out an actual long division, we do use facts about the division of polynomials, namely the Factor Theorem ( http://en.wikipedia.org/wiki/Factor_theorem), which states that if  is a root of a polynomial
is a root of a polynomial  then
then 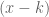 is a factor of
is a factor of  .
.
Now we use what we know about dynamical systems. The roots of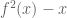 are the period-2 points of
are the period-2 points of 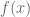 . In particular, the fixed points of
. In particular, the fixed points of 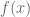 are period-2 points of
are period-2 points of 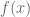 . That is the roots of
. That is the roots of  are also roots of
are also roots of 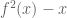 .
.
Now we use the factor theorem. Roots are equivalent to factors: if all the roots of are roots are roots of
are roots are roots of 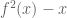 then all the factors of
then all the factors of  are factors of
are factors of 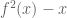 as
as
ROOTS FACTORS
FACTORS
If all the factors of are factors of
are factors of 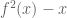 then
then  divides
divides 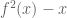

Now adopt this argument to when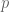 and
and  are any natural numbers. You need the converse of the following theorem:
are any natural numbers. You need the converse of the following theorem:
If is a prime period-
is a prime period-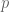 point of a mapping
point of a mapping  , and also a period-
, and also a period- point of
point of 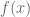 , then
, then 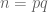 for some
for some  .
.
Regards,
J.P.
April 4, 2012 at 12:26 pm
Student 8
I have one final question, in part g of question 5, what do you mean by describe the limiting behavior?
April 4, 2012 at 12:29 pm
J.P. McCarthy
What happens to the iterates,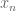 , as
, as  .
.
In other words, find
Regards,
J.P.
April 11, 2012 at 9:22 am
Student 9
I just wanted to ask you a question in relation to the differential calculus question which is question 3. While I was doing the homework Q3 differential calculus I ran into a problem with part (i). I have take that the question is looking for us to pick a function that allows us to generate periodic points based on the values used in the function. I have picked the function as that function based on the result from part (h) and I was hoping that you could tell me if i am going in the right direction with it.
as that function based on the result from part (h) and I was hoping that you could tell me if i am going in the right direction with it.
Kind regards
April 11, 2012 at 9:32 am
J.P. McCarthy
Taking inspiration from parts (d) and (h) we can say that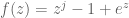 for some
for some  is indeed eventually fixed.
is indeed eventually fixed.
However part (i) wants us to find a function that is a prime-period-
that is a prime-period-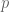 point of
point of  . That is we need a function
. That is we need a function  such that if we differentiate
such that if we differentiate 
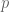 times:
times:
and furthermore none of
From parts (a) and (b) we see that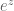 is prime-period-one (or fixed), and
is prime-period-one (or fixed), and  is prime-period-two point. Hence these are answers for
is prime-period-two point. Hence these are answers for 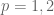 .
.
Compare now these functions with
as mentioned in part 2, and note that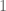 and
and  are primitive first and, respectively, second roots of unity (primitive meaning that
are primitive first and, respectively, second roots of unity (primitive meaning that  is a solution of
is a solution of 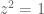 but not
but not  ).
).
Try differentiating three times and solve equal to
three times and solve equal to  …
…
Hopefully that might give you enough to see what to do.
Regards,
J.P.
April 12, 2012 at 11:39 am
Robert Twomey
hi J.P.
just about question 5, part j, did you mean that p^n = I^2? Just wondering if that was a typo, thanks.
April 12, 2012 at 12:24 pm
J.P. McCarthy
Robert,
Sorry this notation isn’t clear you’re right. is the two-by-two identity:
is the two-by-two identity:
Incidentally .
.
Regards,
J.P.
April 12, 2012 at 12:34 pm
Robert Twomey
thanks for clearing that up!
April 17, 2012 at 8:32 am
Student 10
I decided to do Question 1 : For (a)(iii) we are asked to prove it has
a fixed point thus prove it has a period-1 point i think? My
argument is that we are told all of the 3 elements and they are all
prime-period 2 points thus they will begin to repeat after 2 iterates.
In order to prove that a fn has a fixed point it is necessary to prove
there exists solns for f(x)=x. However we know there exists solns for
f2(x)=x because all the elements are prime period 2. Thus its true to
say that the solutions of f2(x)=x will contain fixed points if they
exist? So what i tried to do was divide f(x)-x into f2(x)=x since we
have to work in the general case. However i got a remainder of x^2-x??
Am i on the right track or completely off ?
April 17, 2012 at 8:45 am
J.P. McCarthy
The result that divides into
divides into 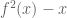 applies (via the Factor Theorem) only when
applies (via the Factor Theorem) only when  is a polynomial. This is not the case here and I have no idea how you divided an abstract
is a polynomial. This is not the case here and I have no idea how you divided an abstract  into
into 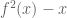 !
!
This result (iii) actually holds whenever has an odd number of elements and there is a clever argument which will give the result.
has an odd number of elements and there is a clever argument which will give the result.
However, with only three elements in we could actually write out ALL of the functions
we could actually write out ALL of the functions  . There are 27 of them. e.g.
. There are 27 of them. e.g.
You could then pick out all the period-2 ones and show that each have a fixed point. This would certainly suffice for an answer.
Obviously this is not ideal but is an option for you. If you do this you might see how the more general argument goes. Funnily enough, the general argument can use an implication of part (iv).
Even by playing around with some of these functions you might see how the general argument goes.
is period-2 and has a fixed point.
Can you find a function that is period-2 and has no fixed point? Explain why not and there is your answer.
Regards,
J.P.
April 18, 2012 at 3:54 pm
Student 11
I have a question about QS1 (B) for the function can you choose any
function? I picked f(x)=x^2?
My question is the second part of (b), just wondering could you help
me on starting it . I know we need some info on number theory to start
it but i can’t think of what it could be ?
April 18, 2012 at 3:57 pm
J.P. McCarthy
For the second part, what is a prime number?
Regards,
J.P.
February 6, 2014 at 5:41 pm
MS3011: Week 5 | J.P. McCarthy: Math Page
[…] Fixed-Point Factor-Theorem (which was called such on the board. It is not in the notes but is found here. When I say examinable you should be able […]