I am emailing a link of this to everyone on the class list every week. If you are not receiving these emails or want to have them sent to another email address feel free to email me at jpmccarthymaths@gmail.com and I will add you to the mailing list.
Continuous Assessment
You are identified by the last four digits of your student number unless you are winning the league. The individual quiz marks are out of 2.5 percentage points. Your best eight quizzes go to the 20% mark for quizzes. The R % column is your running percentage (for best eight quizzes — now this includes missed quizzes — before I was doing the best non-zero but now I am including the zeros if a zero is in your best eight), MPP is your Maple Percentage Points and the GPP is your Gross Percentage Points (for best eight quizzes and Maple). Most of the columns are rounded but column nine, for quiz eight, is correct.
| S/N | Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Q7 | Q8 | Q9 | Q10 | Q11 | R % | QPP | MPP | GPP |
| Kelliher | 3 | 3 | 3 | 3 | 2 | 3 | 3 | 3 | 2.5 | 100 | 20.0 | 7.5 | 27.5 | ||
| Casey | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 2.5 | 100 | 20.0 | 7.5 | 27.5 | ||
| 3281 | 2 | 3 | 3 | 3 | 2 | 3 | 3 | 3 | 2.4 | 99 | 19.8 | 7.5 | 27.3 | ||
| 8335 | 2 | 3 | 2 | 3 | 3 | 3 | 2 | 3 | 2.3 | 98 | 19.6 | 7.5 | 27.1 | ||
| 8416 | 2 | 1 | 2 | 3 | 3 | 1 | 2 | 3 | 2.5 | 91 | 18.1 | 7.5 | 25.6 | ||
| 8403 | 2 | 1 | 2 | 3 | 1 | 2 | 2 | 3 | 2.4 | 87 | 17.4 | 7.5 | 24.9 | ||
| 6548 | 2 | 1 | 2 | 3 | 2 | 2 | 2 | 3 | 2.5 | 87 | 17.3 | 7.5 | 24.8 | ||
| 4198 | 0 | 1 | 2 | 3 | 2 | 3 | 3 | 3 | 2.3 | 86 | 17.2 | 7.5 | 24.7 | ||
| 8478 | 2 | 2 | 2 | 2 | 0 | 3 | 2 | 2 | 2 | 84 | 16.9 | 7.5 | 24.4 | ||
| 7878 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2.2 | 83 | 16.6 | 7.5 | 24.1 | ||
| 1864 | 1 | 2 | 3 | 2 | 1 | 1 | 2 | 3 | 1.15 | 78 | 15.6 | 7.5 | 23.1 | ||
| 8603 | 1 | 2 | 2 | 2 | 0 | 2 | 3 | 2 | 2.3 | 77 | 15.5 | 7.5 | 23.0 | ||
| 2567 | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 2 | 1.9 | 76 | 15.2 | 7.5 | 22.7 | ||
| 8556 | 1 | 1 | 2 | 2 | 0 | 2 | 3 | 3 | 1.2 | 74 | 14.8 | 7.5 | 22.3 | ||
| 1852 | 1 | 1 | 2 | 2 | 2 | 2 | 1 | 1 | 2.1 | 65 | 12.9 | 7.5 | 20.4 | ||
| 5546 | 0 | 0 | 1 | 1 | 2 | 2 | 3 | 2 | 2.5 | 62 | 12.4 | 7.5 | 19.9 | ||
| 8455 | 0 | 1 | 1 | 1 | 2 | 2 | 2 | 1 | 2.2 | 60 | 12.0 | 7.5 | 19.5 | ||
| 2859 | 2 | 1 | 0 | 1 | 2 | 2 | 2 | 3 | 0 | 58 | 11.6 | 7.5 | 19.1 | ||
| 7950 | 0 | 0 | 1 | 0 | 2 | 1 | 3 | 3 | 0 | 44 | 8.8 | 6 | 14.8 | ||
| 9464 | 1 | 1 | 2 | 1 | 1 | 1 | 2 | 0 | 0 | 43 | 8.6 | 6 | 14.6 | ||
| 4775 | 1 | 0 | 1 | 0 | 0 | 1 | 2 | 2 | 1.4 | 43 | 8.6 | 7.5 | 16.1 | ||
| 7209 | 2 | 1 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 28 | 5.5 | 4.5 | 10.0 | ||
| 5553 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 1.3 | 4.5 | 5.8 |
Any students who missed a Maple lab are invited to do the relevant lab in their own time and send their Maple file to me via email.
Quiz 10 Question Bank
This question bank is very large… and I am quite happy with that. I count on P.106 five questions but only three ‘types’. On P.118 there are 12 questions but only four, maybe five ‘types’. I am happy because I want ye to learn and understand the general idea/technique rather than learning off set questions (which in fairness the majority of ye are not doing).
- P. 106, Q.3, 4(i), (ii)
- P. 118, Q.1*, 2 (i), (ii), Q.3 (b), (c), Q.7(i), (ii), Q.8 (a), (b), (c)
*if you look at the Laplace tables at the back of the notes, you will see that there is an alternative way to do Q.1(iii) — either approach will do.
There is no value in writing down the final answers alone — you will receive marks for full and correct solutions — but nothing for final answers without justification or skipping important steps. Please don’t learn off model solutions — you need to understand the material not just on a superficial level to do well later on. Quiz 10 runs from 19:15 to 19:30 sharp on Wednesday 29 April as it is a ‘Maple’ night.
Week 10
We had a busy night in Week 10. We finished the example of taking a differential equation, translating/transforming it into an algebraic equation and solving this transformed equation for the transform of the solution of the original differential equation, . Then we learnt how to send this back to
using the Inverse Laplace Transform. To do these we needed partial fractions so we had a quick review of these. Then we did loads of examples of Inverse Laplace transforms.
Week 11
We will do one more inverse Laplace transform that requires a completing of the square. In the last section we have six examples of full Laplace Transform questions — we will try and do four or five.
Week 12
In Week 12 we will finish off the six examples. Then we will talk about examples — especially to damped harmonic oscillators. If we have extra time left over I will take questions from the class and invite you to do exercises if we run out of exercises.
Week 13
In Week 13 we will go over the exam paper after p.152. We haven’t done Q.1(a) and 2(c) in the same way so I will have alternative questions. I am not going to ask you questions like Q. 1 (d) (ii) and 4. (a) (ii) but I will have alternatives.
Maple Test
The Maple Test will take place on the night of 29 April. I have given ye a sample in class.
Group 1 – Starts at 18:00 and Finishes at 20:50:
- Wednesdays 18:00-19:05 – Maple Test in room C219
- Wednesdays 19:15-19:30 – Weekly Quiz in C212
- Wednesdays 19:30-20.50 – Theory class in room C212
Group 2 – Starts at 19:15 and Finishes at 22:00:
- Wednesdays 19:15-19:30 – Weekly Quiz in C212
- Wednesdays 19:30-20:50 – Theory class in room C212
- Wednesdays 20.55-22:00 – Maple Test in room C219
As you can see here you can download a student copy of Maple. Some students said that they were unable to open the file I sent in their Maple 17 — this is strange as I am actually using Maple 16!
Academic Learning Centre
The word on the Academic Learning Centre is that although the evening session perhaps might have been made exclusive to evening students, the fact of the matter is that they are not.
My departmental head suggested that if a group of ye want to get an improvement in your ALC experience, that ye should email questions to catherine.palmer@cit.ie in advance of the session. Dr Palmer said that this will allow her to more easily help ye.
Study
Please feel free to ask me questions about the exercises via email or even better on this webpage. Anyone can give me exercises they have done and I will correct them. I also advise that you visit the Academic Learning Centre.
Continuous Assessment
The Continuous Assessment is broken into Weekly Quizzes (20%) and Maple (10%). There will be eleven weekly quizzes and your eight best results will count (so 2.5% per quiz from eight quizzes). You will receive an email (i.e. this one) on Thursday/Friday detailing the examinable exercises. Maple consists of five labs and a Maple Test in the sixth lab. Satisfactory participation in labs gives you 1.5% and the Maple Test is worth 2.5%. More on this in the coming days.
Student Resources
Please see the Student Resources tab on the top of this page for information on the Academic Learning Centre, etc..

2 comments
Comments feed for this article
April 27, 2015 at 7:31 am
Student
J.P.,
Just on two questions 1.(iii) & 3.(c); my attempts are attached.
To me these look like laplace transformer of , but from your answers I’m thinking that you rearranged this function to be a laplace transform of some
, but from your answers I’m thinking that you rearranged this function to be a laplace transform of some  ? I can’t seem to see how to get this in terms of
? I can’t seem to see how to get this in terms of 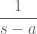 if that’s the way you worked it out?
if that’s the way you worked it out?
Also is there some way of knowing what to look for in these questions, because some of these look like you could go down different routes . (Eg is there only one solution to each problem?)
April 27, 2015 at 7:41 am
J.P. McCarthy
First of all yes the answers are unique. Occasionally the answers might look slightly different but there is only one answer to each question.
Regarding this is NOT a cosine (when transformed back).
this is NOT a cosine (when transformed back).
Note we have
and it HAS to be not
not  .
.
The correct way to approach this is to realise that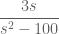 is NOT in the tables therefore we might want to write it as a sum of simpler objects that might be in the tables… this means you must do partial fractions…
is NOT in the tables therefore we might want to write it as a sum of simpler objects that might be in the tables… this means you must do partial fractions…
Therefore factorise the bottom (note so is a difference of two squares) as
so is a difference of two squares) as  . Now we have
. Now we have
using two Rule Is… because it is two Rule Is you may use the Cover-Up Method to find and
and  .
.
ALTERNATIVE METHOD — acceptable but I am not teaching it
I mentioned an alternative using the tables that are at the back of the notes.
You will see that in these tables there is
This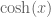 is what is called HYPERBOLIC cosine and is defined by
is what is called HYPERBOLIC cosine and is defined by
where is the imaginary unit that satisfies
is the imaginary unit that satisfies  … now you might think that this different but actually we have
… now you might think that this different but actually we have
so you do get the same answer.
We can see this directly by noting
so
Regards,
J.P.