Student Feedback
You are invited to give your feedback on my teaching and this module here.
Test 2
Test 2, worth 15% of your final grade, based on Chapter 3: Algebra, and will take place on Tuesday 3 December in the usual lecture venue of D160.
The sample is to give you an idea of the length of the test. You know from Test 1 the layout (i.e. you write your answers on the paper). You will be allowed use a calculator for all questions.
I strongly advise you that, for those who might have done poorly, or not particularly well, in Test 1, attending tutorials alone will not be sufficient preparation for this test, and you will have to devote extra time outside classes to study aka do exercises.
If you go into Canvas, and go into MATH6055 and the ‘Algebra’ unit, you might see online practise questions for Test 2.
Week 11
On Monday we half-finished the Examples of Functions (we will finish this off on Friday) mini-chapter before starting the final chapter, the easy chapter, on Network (Graph) Theory.
Week 12
We will finish our study of Graph Theory by looking at Eulerian graphs, Hamiltonian graphs, and Dirac’s Theorem.
The Test is on Tuesday.
Week 13
We will have two review lectures on Monday and Tuesday in the usual times and venues and tutorials as normal.
We will go through the MATH6055 Winter 2018 paper, and then I will answer your questions if there are any. If there are none I will help one-to-one. Usual class times and locations.
CIT Mathematics Exam Papers
These are not always found in your programme selection — most of the time you will have to look here.
Sample Papers
Two sample papers here:
Both Sample Exams should be considered under the following understanding:
This sample has been drafted to give you an idea of the MATH6055 LAYOUT and is no indication of the specifics, difficulty or length of any individual questions.
Academic Learning Centre
If you are a little worried about your maths this semester, perhaps after the Quick Test or in general, I would just like to remind you about the Academic Learning Centre. Most students received slips detailing areas of maths that they should brush up on. The timetable is here.
Study
Please feel free to ask me questions about the exercises via email or even better on this webpage — especially those of us who struggled in the test.
Student Resources
Please see the Student Resources tab on the top of this page for information on the Academic Learning Centre, etc.

2 comments
Comments feed for this article
December 2, 2019 at 8:36 am
Student
Dear J.P.,
I have attached below the questions I have done by myself which I was not able to complete in the tutorial class. The questions in the box are the ones I am stuck on or not sure what to do with.
Can you please have a look at the questions and let me know if they are correct and how to solve them.
Kind regards.
December 2, 2019 at 8:48 am
J.P. McCarthy
Q. 1 Use BEMDAS. Do the multiplication and division before the addition and subtraction:
Q. 2 You did all the hard work but got the answer wrong:
and so the answer is
and not .
.
Q. 3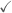
Q. 4 Use the laws of logs (in the table) to write:
and
Now use the other law to write:
Q. 5 a) You went from an equation to a non-equation.
APPLY THE SAME FUNCTION TO BOTH SIDES
I don’t really see why you would want to solve this equal to zero:
The problem is the division by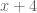 and the division by
and the division by  . Get rid of those and the problem is easier. The appropriate inverse functions are
. Get rid of those and the problem is easier. The appropriate inverse functions are  and
and  , and if we apply both we have
, and if we apply both we have 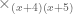 :
:
Work from here.
Q. 5 b)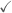
Q. 5 c) Check both answers by substituting into the original equation. Squaring can give extra solutions!
Q. 6 a)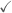
Q. 6 b) You have
This is correct. The inverse of multiplying by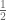 is
is  or
or  . Apply this function to both sides to find
. Apply this function to both sides to find  .
.
Regards,
J.P.