Category Archive

You are currently browsing the category archive for the ‘Probability Theory’ category.

On the number of fixed points of conditioned quantum permutations

March 31, 2024 in Probability Theory, Quantum Groups, Research | Leave a comment

Consider the symmetric group S_N. Let \mathrm{fix}_N \in C(S_N) count the number of fixed points of a permutation \sigma\in S_N. Where X\sim \mathrm{Poi}[1], we have that for a random permutation \xi_N\in S_N chosen with respect to the uniform distribution, the \mathrm{fix}_N converges in distribution to X in the sense that:

\displaystyle \lim_{N\to \infty}\mathbb{P}[\mathrm{fix}_N(\xi_N)=m]=\mathbb{P}[X=m].

In this note we will look at the distribution in the case where the uniform distribution is conditioned on \xi_N(1)=1.

Theorem

Let \xi_N\in S_N be chosen according to the distribution uniform on permutations for which one is a fixed point. The number of fixed points has distribution 1+\mathrm{Poi}[1] in the sense that, where X\sim \mathrm{Poi}[1],

\displaystyle \lim_{N\to \infty}\mathbb{P}[\mathrm{fix}_N(\xi_N)=m]=\mathbb{P}[X=m-1].

Proof: What can be shown, ostensibly from stuff from the quantum permutation side of the house is that, where h_N is integration against the uniform distribution, and \widetilde{h_N} is integration against the uniform distribution on permutations with one a fixed point, that, for k<N:

\displaystyle \widetilde{h_N}(\mathrm{fix}_N^k)=h_N(\mathrm{fix}_N^{k+1})=B_{k+1},

the (k+1)-st Bell number. Now consider the moments of 1+X:

\displaystyle \sum_{t=0}^\infty t^k\mathbb{P}[1+X=t]=\sum_{t=0}^\infty t^k\mathbb{P}[X=t-1]

\displaystyle =\sum_{t=1}^\infty t^k\frac{e^{-1}}{(t-1)!}

\displaystyle \underset{s=t-1}{=}\sum_{s=0}^\infty(s+1)^k\frac{e^{-1}}{s!}

\displaystyle =\sum_{s=0}^\infty\sum_{i=0}^k\binom{k}{i}s^i \frac{e^{-1}}{s!}

\displaystyle =\sum_{i=0}^k\binom{k}{i}\sum_{s=0}^\infty s^i\frac{e^{-1}}{s!}

\displaystyle =\sum_{i=0}^k \binom{k}{i} B_k=B_{k+1},

using the fact that the Bell numbers are the moments of that Poisson distribution and the standard recurrence for the Bell numbers.

Local vs Global Conditioning of Quantum Permutations

In the quantum case we define

\displaystyle \mathrm{fix}_N:=\mathrm{Tr}(u),

where u\in M_N(C(S_N^+)) is the fundamental magic representation. The moments of \mathrm{fix}_N with respect to the Haar state are the Catalan numbers and it follows that the law of \mathrm{fix}_N is a Marchenko-Pastur distribution, with density

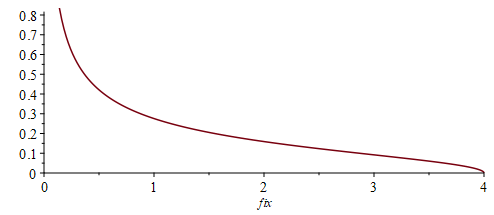
\displaystyle \dfrac{1}{2\pi}\sqrt{\frac{4}{t}-1}:

Note that when we measure the Haar state with some finite spectrum version of \mathrm{fix}_N we find:

  • the probability of finding an integer number of fixed points is zero, and
  • independently of N, the probability of finding more than four fixed points is zero.

In the classical case above when we chose the permutation uniformly from those who fix one, there are two ways of viewing it:

  • we pick an element of S_N that fixes one, OR
  • we consider the isotropy subgroup S_{N-1}\subset S_N and choose our permutation from S_{N-1}.

Classically, these are the same thing. In the quantum case these two things can be interpreted differently. The second case is quite clear in the quantum case. For N>4, we take the isotropy S_{N-1}^+\subset S_N^+ via the quotient C(S_N^+)\to C(S_N^+)/\langle1-u_{11}\rangle.

The analogue of the uniform distribution on S_{N-1}\subset S_N here is the Haar idempotent h_{C(S_{N-1}^+)}\circ \pi. Note this maps \mathrm{fix}_N to 1+\mathrm{fix}_{N-1}. Now, using the fact that h_{C(S_{N-1}^+)}(\mathrm{fix}_{N-1})=C_k, the Catalan number, we have that the moments of \mathrm{fix}_N with respect to h_{C(S_{N-1}^+)}\circ \pi is the binomial transform of the Catalan numbers (the binomial transform of B_1,\dots,B_k is B_{k+1}). It follows, using similar stuff to the above, that the distribution of \mathrm{fix}_N with respect to h_{C(S_{N-1}^+)}\circ \pi is just a shifted version of Marchenko–Pastur:

I guess this is marginally more interesting than the unshifted version.

Now, what about an analogue of “we pick an element of S_N that fixes one”. So if we take the Haar state and measure the observable u_{11}\in C(S_N^+) that asks of a quantum permutation, does it fix one, we get, conditioned on this, the state:

\displaystyle h_1(f):=N\cdot h(u_{11}fh_{11})=\dfrac{h(u_{11}fu_{11})}{h(u_{11})}\qquad (f\in C(S_N^+)).

And, it turns out, as above, using stuff from the quantum permutation side of the house:

\displaystyle h_1(\mathrm{fix}_N^k)=h(\mathrm{fix}_N^{k+1})=C_{k+1}.

Quite quickly from here we find that the density of the distribution of \mathrm{fix}_N with respect to h_1 is

\displaystyle \frac{t}{2\pi}\sqrt{\frac{4}{t}-1}

This is so interesting:

  • it doesn’t change the support — we still find between 0 and 4 fixed points,
  • we have a new symmetry about \mathrm{fix}_N=2, we had another unexpected symmetry here.
  • the mean jumps from one to two, that is not unexpected, but
  • the mode jumps from zero to two!
  • even though we have observed one to one, there can still be less than one fixed point when we measure… and this happens with probability \approx 1/5.

The next obvious question is what happens with:

\displaystyle f\mapsto \dfrac{h_1(u_{22}fu_{22})}{h_1(u_{22})}\qquad (f\in C(S_N^+))

Epilogue?

So what about this local vs global conditioning? Well, no matter what subsequent measurements are made to h_{C(S_{N-1}^+)}\circ \pi, we will always find that one is a fixed point. That conditioning is ‘global’.

This is not the case with h_1, and why the support of the law is not bounded above one, like that of the globally conditioned h_{C(S_{N-1}^+)}\circ \pi. In fact, there is a non-zero probability that h_1 is observed to fix two but then subsequently not fix one anymore. That conditioning was only local: the probability that h_1 fixes one is 100%… but subsequent measurements can destroy that conditioning… it is only local.

A strange property of quantum permutations

February 13, 2024 in Probability Theory, Quantum Groups, Research | Leave a comment

Classical Warm-up

Let S_N be the classical permutation group on N symbols. The algebra of continuous functions C(S_N) on S_N is generated by indicator functions:

\displaystyle \mathbf{1}_{j\to i}(\sigma)=\delta_{i,\sigma(j)}.

This algebra is commutative, but we will use some non-commutative algebraic analogues. Let \widetilde{\pi}\in M_p(S_N) be the uniform probability distribution on S_N and by \pi the associated state on C(S_N):

\displaystyle\pi(f)=\sum_{t\in G}f(t)\,\widetilde{\pi}(\{t\})=\frac{1}{|S_N|}\sum_{t\in G} f(t)\qquad (f\in C(S_N))

When choosing a permutation at random what is the probability that it sends 1\to 1? Well, this will equal, in some notation we won’t fully explain here:

\displaystyle \mathbb{P}[\pi(1)=1]=\pi(\mathbf{1}_{1\to 1})=\frac{1}{N}.

Once this has been observed, there is a conditioning of the state \pi\mapsto \pi_{1\to 1}:

\displaystyle \pi_{1\to 1}(f)=\dfrac{\pi(\mathbf{1}_{1\to 1}f\mathbf{1}_{1\to 1} )}{\pi(\mathbf{1}_{1\to 1})}=N \pi(\mathbf{1}_{1\to 1}f\mathbf{1}_{1\to 1} )) \qquad (f\in C(S_N)).

The state was given by \pi but is now given by \pi_{1\to 1}. Now, after having observed this random permutation mapping 1\to 1, we can ask it another question.

Consider a subset S\subseteq \{3,\dots,N\} and define:

\displaystyle\mathbf{1}_{3\to S}:=\sum_{s\in S}\mathbf{1}_{3\to s}.

This is an observable, which basically asks of a permutation, do you map three into S? One for yes, zero for no. So let us ask this of \pi_{1\to 1}:

What is the probability that a random permutation maps three into S after having been observed mapping one to one?

We find, with a fairly elementary calculation that the answer to this question is:

\displaystyle \mathbb{P}[\pi_{1\to 1}(3)\in S]=\frac{|S|}{N-1}.

If \pi_{1\to 1}(3)\in S, we get further conditioning, to let us say \nu:

\displaystyle \nu(f)=\frac{N(N-1)}{|S|}\pi(\mathbf{1}_{1\to 1}\mathbf{1}_{3\to S}f\mathbf{1}_{3\to S}\mathbf{1}_{1\to 1})\qquad (f\in C(S_N))

What is the probability that after seeing \pi_{1\to 1}(3)\in S after \pi(1)=1 we see \nu(2)=2? We find it is:

\displaystyle \mathbb{P}[\nu(2)=2]=\frac{1}{N-2}.

Therefore, where \succ means after, and the state-conditioning implicit

\displaystyle \mathbb{P}[(\pi(2)=2)\succ (\pi(3)\in S)\succ(\pi(1)=1)]

\displaystyle =\frac{1}{N}\cdot \frac{|S|}{N-1}\cdot\frac{1}{N-2}=\frac{|S|}{N(N-1)(N-2)}

Now let us ask a ridiculous question. What was the probability that \nu(1)=2? But \nu is just a conditioning of \pi_{1\to 1}, which mapped one to one with probability one:

\displaystyle \mathbb{P}[\pi_{1\to 1}(1)=1]=\dfrac{\pi(\mathbf{1}_{1\to 1}\mathbf{1}_{1\to 1}\mathbf{1}_{1\to 1})}{\pi(\mathbf{1}_{1\to 1})}=1.

Of course the answer is zero. Can we actually see it in the above framework: well, yes, because the algebra of functions is commutative. You end up with evaluating a state at

\displaystyle \mathbf{1}_{1\to 1}\mathbf{1}_{3\to S}\mathbf{1}_{1\to 2}\mathbf{1}_{3\to S}\mathbf{1}_{1\to 1},

but commutativity sees \mathbf{1}_{1\to 1}\mathbf{1}_{1\to 2}… and no permutation maps one to one and one to two (you’d need a relation to do that), and so \mathbf{1}_{1\to 1}\mathbf{1}_{1\to 2}=0, so is the length five monomial above, and so is the probability we spoke about.

We don’t have to do state conditioning and multiplication to calculate the probability that a random permutation maps one to one, then maps three into S, then maps two to two though. Where |f|^2=f^*f:

\displaystyle \mathbb{P}[(\pi(2)=2)\succ (\pi(3)\in S)\succ(\pi(1)=1)]

=\pi(|\mathbf{1}_{2\to 2}\mathbf{1}_{3\to S}\mathbf{1}_{1\to 1}|^2)=\dfrac{|S|}{N(N-1)(N-2)}.

Let us remark that this probability is increasing in |S|\in\{0,1,\dots,N-2\}: the less we specify about the event, in this case represented by the projection \mathbf{1}_{3\to S}, the more general it is, the larger the probability.

Let’s Go Quantum

In the case of quantum permutations, so talking S_N^+ the ridiculous question of asking what is the probability that a quantum permutation maps one to two after it had previously mapped one to one… is no longer zero. Where q(N)=N(N-1)(N^2-4N+2), the probability of the analogue of a “random” quantum permutation, the Haar state h doing this is:

\displaystyle \mathbb{P}[(h(1)=2)\succ(h(3)=3)\succ (h(1=1))]=\frac{N-3}{q(N)}

Anyway, the quantum versions of the \mathbf{1}_{j\to i} are entries u_{ij}\in M_N(C(S_N^+)) of a universal magic unitary. We say:

\mathbb{P}[(h(2)=2)\succ (h(3)\in S)\succ (h(1)=1)]:=h(|u_{22}u_{S,3}u_{11}|^2),

where u_{S,3}=\sum_{s\in S}u_{s3}. We find this probability is:

\displaystyle \mathbb{P}[(h(2)=2)\succ (h(3)\in S)\succ (h(1)=1)]=\frac{|S|(N^2-5N+5+|S|)}{(N-2)q(N)}.

This is also increasing in |S|. Again, the less specificity about the event, the greater the probability.

This quantity is related to the classical probability above, and there are asymptotic similarities. Writing |S|=N-2-|S^c|, where S^c is the complement of S in \{3,4,\dots,N\}:

\displaystyle \mathbb{P}[(h(2)=2)\succ (h(3)\in S)\succ (h(1)=1)]

\displaystyle=\mathbb{P}[(\pi(2)=2)\succ (\pi(3)\in S)\succ(\pi(1)=1)]\cdot\left[1-\frac{|S^c|+1}{q(N)}\right]

I guess this also says, the larger |S|, the more similar the classical and quantum probabilities.

A twist

What if instead of looking at h(2)=2 after h(3)\in S after h(1)=1 but instead we asked about h(1)=2? This should be non-zero, but what is the dependence on |S|?

From our classical intuition, we would probably just expect, well, the same really. The larger the value of |S|, the less we are saying about the event. The larger the probability. But in fact this is not the case. The probability is largest when |S| is close to (N-2)/2. We will write down the probability, and then explain, mathematically, why the symmetry with respect to |S|\leftrightarrow N-2-|S|, with respect to S\leftrightarrow S^c:

\displaystyle \mathbb{P}[(h(1)=2)\succ (h(3)\in S)\succ (h(1)=1)]=\dfrac{|S|(N-2-|S|)}{q(N)}.

Proof: Consider u_{21}u_{11}=0. Insert between them 1_{C(S_N^+)}=\sum_{k=1}^Nu_{k3}:

\displaystyle u_{21}\sum_{k=1}^Nu_{k3} u_{11}=\sum_{k=1}u_{21}u_{k3}u_{11}=0.

Like in the classical case, by definition here, u_{21}u_{23}=0=u_{13}u_{11}=0. So split into two sums:

\displaystyle \sum_{s\in S}u_{21}u_{i3}u_{11}+\sum_{j\in S^c}u_{21}u_{j3}u_{11}=0.

Now, classically, this is just a sum of zero terms equal to zero, but not in the quantum world where we have these u_{21}u_{j3}u_{11}\neq 0. They are not positive though. We can now split:

\displaystyle \sum_{s\in S}u_{21}u_{i3}u_{11}=-\sum_{j\in S^c}u_{21}u_{j3}u_{11}.

Now take the |\cdot|^2 of both sides to show that:

\displaystyle |u_{21}u_{S,3}u_{11}|^2=|u_{21}u_{S^c,3}u_{11}|^2

This yields the strange probability above. I think any intuition I have for this would be very much post-hoc. I think I will just let it hang there as something weird, cool and mysterious about quantum permutations…

A probability question on card shuffling

November 17, 2023 in General, Probability Theory | Leave a comment

Alice, Bob and Carol are hanging around, messing with playing cards.

Alice and Bob each have a new deck of cards, and Alice, Bob, and Carol all know what order the decks are in.

Carol has to go away for a few hours.

Alice starts shuffling the deck of cards with the following weird shuffle: she selects two (different) cards at random, and swaps them. She does this for hours, doing it hundreds and hundreds of times.

Bob does the same with his deck.

Carol comes back and asked “have you mixed up those decks yet?” A deck of cards is “mixed up” if each possible order is approximately equally likely:

\displaystyle \mathbb{P}[\text{ deck in order }\sigma\in S_{52}]\approx \frac{1}{52!}

She asks Alice how many times she shuffled the deck. Alice says she doesn’t know, but it was hundreds, nay thousands of times. Carol says, great, your deck is mixed up!

Bob pipes up and says “I don’t know how many times I shuffled either. But I am fairly sure it was over a thousand”. Carol was just about to say, great job mixing up the deck, when Bob interjects “I do know that I did an even number of shuffles though.“.

Why does this mean that Bob’s deck isn’t mixed up?

The Ergodic Theorem for Random Walks on Finite Quantum Groups

April 2, 2020 in C*-Algebras & Operator Theory, Probability Theory, Quantum Groups, Random Walks on Finite Quantum Groups, Research, Research Updates | 1 comment

Abstract

Necessary and sufficient conditions for a Markov chain to be ergodic are that the chain is irreducible and aperiodic. This result is manifest in the case of random walks on finite groups by a statement about the support of the driving probability: a random walk on a finite group is ergodic if and only if the support is not concentrated on a proper subgroup, nor on a coset of a proper normal subgroup. The study of random walks on finite groups extends naturally to the study of random walks on finite quantum groups, where a state on the algebra of functions plays the role of the driving probability. Necessary and sufficient conditions for ergodicity of a random walk on a finite quantum group are given on the support projection of the driving state.

Link to journal here.

Irreducible and Periodic Positive Maps

November 14, 2019 in C*-Algebras & Operator Theory, Probability Theory, Research | 1 comment

In my pursuit of an Ergodic Theorem for Random Walks on (probably finite) Quantum Groups, I have been looking at analogues of Irreducible and Periodic. I have, more or less, got a handle on irreducibility, but I am better at periodicity than aperiodicity.

The question of how to generalise these notions from the (finite) classical to noncommutative world has already been considered in a paper (whose title is the title of this post) of Fagnola and Pellicer. I can use their definition of periodic, and show that the definition of irreducible that I use is equivalent. This post is based largely on that paper.

Introduction

Consider a random walk on a finite group G driven by \nu\in M_p(G). The state of the random walk after k steps is given by \nu^{\star k}, defined inductively (on the algebra of functions level) by the associative

\nu\star \nu=(\nu\otimes\nu)\circ \Delta.

The convolution is also implemented by right multiplication by the stochastic operator:

\nu\star \nu=\nu P,

where P\in L(F(G)) has entries, with respect to a basis (\delta_{g_i})_{i\geq 1} P_{ij}=\nu(g_jg_{i^{-1}}). Furthermore, therefore

\nu^{\star k}=\varepsilon P^k,

and so the stochastic operator P describes the random walk just as well as the driving probabilty \nu.

The random walk driven by \nu is said to be irreducible if for all g_\ell\in G, there exists k\in\mathbb{N} such that (if g_1=e) [P^k]_{1\ell}>0.

The period of the random walk is defined by:

\displaystyle \gcd\left(d\in\mathbb{N}:[P^d]_{11}>0\right).

The random walk is said to be aperiodic if the period of the random walk is one.

These statements have counterparts on the set level.

If P is not irreducible, there exists a proper subset of G, say S\subsetneq G, such that the set of functions supported on S are P-invariant.  It turns out that S is a proper subgroup of G.

Moreover, when P is irreducible, the period is the greatest common divisor of all the natural numbers d such that there exists a partition S_0, S_1, \dots, S_{d-1} of G such that the subalgebras A_k of functions supported in S_k satisfy:

P(A_k)=A_{k-1} and P(A_{0})=A_{d-1} (slight typo in the paper here).

In fact, in this case it is necessarily the case that \nu is concentrated on a coset of a proper normal subgroup N\rhd G, say gN. Then S_k=g^kN.

Suppose that f is supported on g^kN. We want to show that for Pf\in A_{k-1}. Recall that 

\nu^{\star k-1}P(f)=\nu^{\star k}(f).

This shows how the stochastic operator reduces the index P(A_k)=A_{k-1}.

A central component of Fagnola and Pellicer’s paper are results about how the decomposition of a stochastic operator:

P(f)=\sum_{\ell}L_\ell^*fL_{\ell},

specifically the maps L_\ell can speak to the irreducibility and periodicity of the random walk given by P. I am not convinced that I need these results (even though I show how they are applicable).

Stochastic Operators and Operator Algebras

Let F(X) be a \mathrm{C}^*-algebra (so that X is in general a  virtual object). A \mathrm{C}^*-subalgebra F(Y) is hereditary if whenever f\in F(X)^+ and h\in F(Y)^+, and f\leq h, then f\in F(Y)^+.

It can be shown that if F(Y) is a hereditary subalgebra of F(X) that there exists a projection \mathbf{1}_Y\in F(X) such that:

F(Y)=\mathbf{1}_YF(X)\mathbf{1}_Y.

All hereditary subalgebras are of this form.

Read the rest of this entry »

A Condition for Convergence of Random Walks on Quantum Groups

November 13, 2018 in Probability Theory, Quantum Groups, Random Walks on Finite Quantum Groups, Research | Leave a comment

In a recent preprint, Haonan Zhang shows that if \nu\in M_p(Y_n) (where Y_n is a Sekine Finite Quantum Group), then the convolution powers, \nu^{\star k}, converges if

\nu(e_{(0,0)})>0.

The algebra of functions F(Y_n) is a multimatrix algebra:

F(Y_n)=\left(\bigoplus_{i,j\in\mathbb{Z}_n}\mathbb{C}e_{(i,j)}\right)\oplus M_n(\mathbb{C}).

As it happens, where a=\sum_{i,j\in\mathbb{Z}_n}x_{(i,j)}e_{(i,j)}\oplus A, the counit on F(Y_n) is given by \varepsilon(a)=x_{(0,0)}, that is \varepsilon=e^{(0,0)}, dual to e_{(0,0)}.

To help with intuition, making the incorrect assumption that Y_n is a classical group (so that F(Y_n) is commutative — it’s not), because \varepsilon=e^{(0,0)}, the statement \nu(e_{(0,0)})>0, implies that for a real coefficient x^{(0,0)}>0,

\nu=x^{(0,0)}\varepsilon+\cdots= x^{(0,0)}\delta^e+\cdots,

as for classical groups \varepsilon=\delta^e.

That is the condition \nu(e_{(0,0)})>0 is a quantum analogue of e\in\text{supp}(\nu).

Consider a random walk on a classical (the algebra of functions on G is commutative) finite group G driven by a \nu\in M_p(G).

The following is a very non-algebra-of-functions-y proof that e\in \text{supp}(\nu) implies that the convolution powers of \nu converge.

Proof: Let H be the smallest subgroup of G on which \nu is supported:

\displaystyle H=\bigcap_{\underset{\nu(S_i)=1}{S_i\subset G}}S_i.

We claim that the random walk on H driven by \nu is ergordic (see Theorem 1.3.2).

The driving probability \nu\in M_p(G) is not supported on any proper subgroup of H, by the definition of H.

If \nu is supported on a coset of proper normal subgroup N, say Nx, then because e\in \text{supp}(\nu), this coset must be Ne\cong N, but this also contradicts the definition of H.

Therefore, \nu^{\star k} converges to the uniform distribution on H \bullet

Apart from the big reason — that this proof talks about points galore — this kind of proof is not available in the quantum case because there exist \nu\in M_p(G) that converge, but not to the Haar state on any quantum subgroup. A quick look at the paper of Zhang shows that some such states have the quantum analogue of e\in\text{supp}(\nu).

So we have some questions:

  • Is there a proof of the classical result (above) in the language of the algebra of functions on G, that necessarily bypasses talk of points and of subgroups?
  • And can this proof be adapted to the quantum case?
  • Is the claim perhaps true for all finite quantum groups but not all compact quantum groups?

Probabilities concentrated on Quantum Subgroups

November 6, 2018 in Probability Theory, Quantum Groups, Random Walks on Finite Quantum Groups, Research | Leave a comment

Quantum Subgroups

Let C(G) be a the algebra of functions on a finite or perhaps compact quantum group (with comultiplication \Delta) and \nu\in M_p(G) a state on C(G). We say that a quantum group H with algebra of function C(H) (with comultiplication \Delta_H) is a quantum subgroup of G if there exists a surjective unital *-homomorphism \pi:C(G)\rightarrow C(H) such that:

\displaystyle \Delta_H\circ \pi=(\pi\otimes \pi)\circ \Delta.

The Classical Case

In the classical case, where the algebras of functions on G and H are commutative,

\displaystyle \pi(\delta_g)=\left\{\begin{array}{cc}\delta_g & \text{ if }g\in H \\ 0 & \text{ otherwise}\end{array}\right..

There is a natural embedding, in the classical case, if H is open (always true for G finite) (thanks UwF) of \imath: C(H) \xrightarrow\, C(G),

\displaystyle \sum_{h\in H}a_h \delta_h \mapsto \sum_{g\in G} a_g \delta_g,

with a_g=a_h for h\in G, and a_g=0 otherwise.

Furthermore, \pi is has the property that

\pi\circ\imath\circ \pi=\pi,

which resembles \pi^2=\pi.

In the case where \nu is a probability on a classical group G, supported on a subgroup H, it is very easy to see that convolutions \nu^{\star k} remain supported on H. Indeed, \nu^{\star k} is the distribution of the random variable

\xi_k=\zeta_k\cdots \zeta_2\cdot \zeta_1,

where the i.i.d. \zeta_i\sim \nu. Clearly \xi_k\in H and so \nu^{\star k} is supported on H.

We can also prove this using the language of the commutative algebra of functions on G, C(G). The state \nu\in M_p(G) being supported on H implies that

\nu\circ\imath\circ \pi=\nu\imath\pi=\nu.

Consider now two probabilities on G but supported on H, say \mu,\,\nu. As they are supported on H we have

\mu=\mu\imath\pi and \nu=\nu\imath\pi.

Consider

(\mu\star \nu)\imath\pi=(\mu\otimes \nu)\circ \Delta\circ \imath\pi

=((\mu\imath\pi)\otimes(\nu\imath\pi))\circ \Delta\circ\imath\pi =(\mu\imath\otimes \nu\imath)(\pi\circ \pi)\Delta\circ\imath\pi

=(\mu\imath\otimes\nu\imath)(\Delta_H\circ \pi\circ \imath\circ \pi)=(\mu\imath\otimes\nu\imath)(\Delta_H\circ \pi)

=(\mu\imath\otimes \nu\imath)\circ (\pi\circ \pi)\circ\Delta=(\mu\imath\pi\otimes \nu\imath\pi)\circ\Delta

=(\mu\otimes\nu)\circ\Delta=\mu\star \nu,

that is \mu\star \nu is also supported on H and inductively \nu^{\star k}.

Some Questions

Back to quantum groups with non-commutative algebras of functions.

  • Can we embed C(H) in C(G) with a map \imath and do we have \pi\circ \imath\circ \pi=\pi, giving the projection-like quality to \pi?
  • Is \nu\circ\imath\circ \pi=\nu a suitable definition for \nu being supported on the subgroup H.

If this is the case, the above proof carries through to the quantum case.

  • If there is no such embedding, what is the appropriate definition of a \nu\in M_p(G) being supported on a quantum subgroup H?
  • If \pi does not have the property of \pi\circ \imath\circ \pi=\pi, in this or another definition, is it still true that \nu being supported on H implies that \nu^{\star k} is too?

Edit

UwF has recommended that I look at this paper to improve my understanding of the concepts involved.

General Mathematical Audience Talk: The Diaconis-Shahshahani Upper Bound Lemma for Finite Quantum Groups

September 1, 2018 in Probability Theory, Quantum Groups, Random Walks on Finite Quantum Groups, Research, Research Updates | Leave a comment

Slides of a talk given at the Irish Mathematical Society 2018 Meeting at University College Dublin, August 2018.

Abstract Four generalisations are used to illustrate the topic. The generalisation from finite “classical” groups to finite quantum groups is motivated using the language of functors (“classical” in this context meaning that the algebra of functions on the group is commutative). The generalisation from random walks on finite “classical” groups to random walks on finite quantum groups is given, as is the generalisation of total variation distance to the quantum case. Finally, a central tool in the study of random walks on finite “classical” groups is the Upper Bound Lemma of Diaconis & Shahshahani, and a generalisation of this machinery is used to find convergence rates of random walks on finite quantum groups.

Projection Distance Equal to Total Variation Distance?

November 9, 2017 in C*-Algebras & Operator Theory, Probability Theory, Quantum Groups, Random Walks on Finite Quantum Groups, Research | 2 comments

Distances between Probability Measures

Let G be a finite quantum group and M_p(G) be the set of states on the \mathrm{C}^\ast-algebra F(G).

The algebra F(G) has an invariant state \int_G\in\mathbb{C}G=F(G)^\ast, the dual space of F(G).

Define a (bijective) map \mathcal{F}:F(G)\rightarrow \mathbb{C}G, by

\displaystyle \mathcal{F}(a)b=\int_G ba,

for a,b\in F(G).

Then, where \|\cdot\|_1^{F(G)}=\int_G|\cdot| and \|\cdot\|_\infty^{F(G)}=\|\cdot\|_{\text{op}}, define the total variation distance between states \nu,\mu\in M_p(G) by

\displaystyle \|\nu-\mu\|=\frac12 \|\mathcal{F}^{-1}(\nu-\mu)\|_1^{F(G)}.

(Quantum Total Variation Distance (QTVD))

Standard non-commutative \mathcal{L}^p machinary shows that:

\displaystyle \|\nu-\mu\|=\sup_{\phi\in F(G):\|\phi\|_\infty^{F(G)}\leq 1}\frac12|\nu(\phi)-\mu(\phi)|.

(supremum presentation)

In the classical case, using the test function \phi=2\mathbf{1}_S-\mathbf{1}_G, where S=\{\nu\geq \mu\}, we have the probabilists’ preferred definition of total variation distance:

\displaystyle \|\nu-\mu\|_{\text{TV}}=\sup_{S\subset G}|\nu(\mathbf{1}_S)-\mu(\mathbf{1}_S)|=\sup_{S\subset G}|\nu(S)-\mu(S)|.

In the classical case the set of indicator functions on the subsets of the group exhaust the set of projections in F(G), and therefore the classical total variation distance is equal to:

\displaystyle \|\nu-\mu\|_P=\sup_{p\text{ a projection}}|\nu(p)-\mu(p)|.

(Projection Distance)

In all cases the quantum total variation distance and the supremum presentation are equal. In the classical case they are equal also to the projection distance. Therefore, in the classical case, we are free to define the total variation distance by the projection distance.

Quantum Projection Distance \neq Quantum Variation Distance?

Perhaps, however, on truly quantum finite groups the projection distance could differ from the QTVD. In particular, a pair of states on a M_n(\mathbb{C}) factor of F(G) might be different in QTVD vs in projection distance (this cannot occur in the classical case as all the factors are one dimensional).

Read the rest of this entry »

Talk: The Diaconis-Shahshahani Upper Bound Lemma for Finite Quantum Groups

May 21, 2017 in Probability Theory, Quantum Groups, Random Walks on Finite Quantum Groups, Research, Research Updates | 1 comment

Slides of a talk given at the Topological Quantum Groups and Harmonic Analysis workshop at Seoul National University, May 2017.

Abstract A central tool in the study of ergodic random walks on finite groups is the Upper Bound Lemma of Diaconis & Shahshahani. The Upper Bound Lemma uses the representation theory of the group to generate upper bounds for the distance to random and thus can be used to determine convergence rates for ergodic walks. These ideas are generalised to the case of finite quantum groups.