Category Archive

You are currently browsing the category archive for the ‘MATH6037’ category.

Basic Control Theory: Part I

March 24, 2015 in General, MATH6037 | Leave a comment

This is the first in a series of posts that are an attempt by me to understand why my Industrial Measurement and Control students need to study the Laplace Transform.

Consider a black box model that takes as an input signal a function x(t) and produces an output signal y(t). For reasons that are as of yet not clear to me, we can take all of the derivatives of y(t) (and x(t)) to vanish for t=0.

Definition

The transfer function of a black box model is defined as

\displaystyle H(s)=\frac{Y(s)}{X(s)},

where Y(s) and X(s) are the Laplace Transforms of y(t) and x(t).

Note we have the Laplace transform of a function f(t) is a function F(s) defined by

F(s)=\mathcal{L}\{f(t)\}=\int_{0}^\infty f(t)e^{-st}\,dt.

Poles of H(s) are complex numbers z such that X(z)=0. For example, for an input signal x(t)=e^t, the transfer function has a pole at s=1 as

\displaystyle F(s)=\frac{1}{s-1}.

If the coefficients of x(t) are real, then in general the poles of the transfer are real or come in conjugate root pairs.

Read the rest of this entry »

MATH6037: Week 7

March 23, 2015 in MATH6037 | 4 comments

I am emailing a link of this to everyone on the class list every week. If you are not receiving these emails or want to have them sent to another email address feel free to email me at jpmccarthymaths@gmail.com and I will add you to the mailing list.

Continuous Assessment

You are identified by the last four digits of your student number unless you are winning the league. The individual quiz marks are out of 2.5 percentage points. Your best eight quizzes go to the 20% mark for quizzes. The R % column is your running percentage (for best eight quizzes), MPP is your Maple Percentage Points and the GPP is your Gross Percentage Points (for best eight quizzes and Maple). Most of the columns are rounded but column six, for quiz five, is correct.

S/N Q1 Q2 Q3 Q4 Q5 Q6 Q7 Q8 Q9 Q10 Q11 R % QPP MPP GPP
Kelliher 3 3 3 3 2.3 98 12.3 4.5 16.8
8335 2 3 2 3 2.5 98 12.3 4.5 16.8
3281 2 3 3 3 2.1 96 12.0 4.5 16.5
5527 2 3 3 3 2.5 94 11.9 4.5 16.4
7878 2 2 2 2 2.1 85 10.6 4.5 15.1
8416 2 1 2 3 2.5 84 10.5 4.5 15.0
8478 2 2 2 2 0 82 8.2 4.5 12.7
1864 1 2 3 2 1.24 76 9.5 4.5 14.0
8403 2 1 2 3 1.3 76 9.5 4.5 14.0
4198 0 1 2 3 1.7 74 7.4 4.5 11.9
6548 2 1 2 3 1.6 71 8.9 4.5 13.4
8603 1 2 2 2 0 67 6.7 3 9.7
8556 1 1 2 2 0 66 6.6 4.5 11.1
2567 2 2 2 1 1.8 65 8.2 4.5 12.7
1852 1 1 2 2 2.1 57 7.1 4.5 11.6
2859 2 1 0 1 1.6 55 5.5 4.5 10.0
5546 0 0 1 1 1.9 53 4.0 4.5 8.5
7950 0 0 1 0 1.8 52 2.6 3 5.6
9464 1 1 2 1 1.24 46 5.7 4.5 10.2
7209 2 1 2 1 0.16 44 5.5 4.5 10.0
8455 0 1 1 1 1.9 38 4.8 4.5 9.3
4775 1 0 1 0 0.4 22 2.2 4.5 6.7
5553 0 1 0 0 0.1 17 1.3 4.5 5.8

Read the rest of this entry »

MATH6037: Week 5

March 5, 2015 in MATH6037 | 10 comments

I am emailing a link of this to everyone on the class list every week. If you are not receiving these emails or want to have them sent to another email address feel free to email me at jpmccarthymaths@gmail.com and I will add you to the mailing list.

Continuous Assessment

You are identified by the last four digits of your student number unless you are winning the league. The individual quiz marks are out of 2.5 percentage points. Your best eight quizzes go to the 20% mark for quizzes. The R % column is your running percentage (for best eight quizzes), MPP is your Maple Percentage Points and the GPP is your Gross Percentage Points (for best eight quizzes and Maple). Most of the columns are rounded but column five, for quiz four, is correct.

S/N Q1 Q2 Q3 Q4 Q5 Q6 Q7 Q8 Q9 Q10 Q11 R % QPP MPP GPP
Kelliher 3 3 3 2.5 100 10.0 3 13.0
3281 2 3 3 2.5 99 9.9 3 12.9
8335 2 3 2 2.5 98 9.8 3 12.8
5527 2 3 3 2.5 94 9.4 3 12.4
7878 2 2 2 1.9 85 8.5 3 11.5
1864 1 2 3 2.1 83 8.3 3 11.3
8403 2 1 2 2.5 82 8.2 3 11.2
8478 2 2 2 2.4 82 8.2 3 11.2
8416 2 1 2 2.5 80 8.0 3 11.0
4198 0 1 2 2.5 76 5.7 3 8.7
6548 2 1 2 2.5 73 7.3 3 10.3
8603 1 2 2 2.4 67 6.7 3 9.7
8556 1 1 2 2.2 66 6.6 3 9.6
2567 2 2 2 1.28 64 6.4 3 9.4
7209 2 1 2 0.5 54 5.4 3 8.4
2859 2 1 0 0.5 52 3.9 3 6.9
1852 1 1 2 1.5 50 5.0 3 8.0
9464 1 1 2 0.9 45 4.5 3 7.5
5546 0 0 1 1 42 2.1 3 5.1
7950 0 0 1 0 32 0.8 1.5 2.3
8455 0 1 1 0.7 29 2.9 3 5.9
5553 0 1 0 0 24 1.2 3 4.2
4775 1 0 1 0 24 1.8 3 4.8

Read the rest of this entry »

MATH6037: Week 4

February 26, 2015 in MATH6037 | 2 comments

I am emailing a link of this to everyone on the class list every week. If you are not receiving these emails or want to have them sent to another email address feel free to email me at jpmccarthymaths@gmail.com and I will add you to the mailing list.

Continuous Assessment

You are identified by the last four digits of your student number unless you are winning the league. The individual quiz marks are out of 2.5 percentage points. Your best eight quizzes go to the 20% mark for quizzes. The R % column is your running percentage (for best eight quizzes), MPP is your Maple Percentage Points and the GPP is your Gross Percentage Points (for best eight quizzes and Maple). The first two columns are rounded figures but the third, for quiz three, is correct.

The solutions to the last quiz may be found in the notes.

S/N Q1 Q2 Q3 Q4 Q5 Q6 Q7 Q8 Q9 Q10 Q11 R % QPP MPP GPP
Kelliher 3 3 2.5 100 7.5 1.5 9
3281 2 3 2.5 98.7 7.4 1.5 8.9
8335 2 3 2.4 97 7.275 1.5 8.775
5527 2 3 2.5 92 6.9 1.5 8.4
7878 2 2 2.25 88 6.6 1.5 8.1
1864 1 2 2.5 82.7 6.2 1.5 7.7
8478 2 2 2.15 76.9 5.77 1.5 7.27
8403 2 1 2.45 76 5.7 1.5 7.2
8416 2 1 2.2 73.3 5.5 1.5 7
2567 2 2 2.05 68 5.1 1.5 6.6
7209 2 1 1.75 64.7 4.85 1.5 6.35
6548 2 1 2.25 64 4.8 1.5 6.3
8556 1 1 2.4 58 4.35 1.5 5.85
NR 1 2 1.85 56.7 4.25 1.5 5.75
9464 1 1 1.5 48 3.6 1.5 5.1
1852 1 1 1.6 46.7 3.5 1.5 5
2859 2 1 0 68 3.4 1.5 4.9
4198 0 1 2 64 3.2 1.5 4.7
8455 0 1 1.05 28.7 2.15 1.5 3.65
4775 1 0 1 24 1.8 1.5 3.3
5553 0 1 0 24 1.2 1.5 2.7
5546 0 0 1.1 44 1.1 1.5 2.6
7950 0 0 0.8 32 0.8 0 0.8

Read the rest of this entry »

MATH6037: Week 3

February 20, 2015 in MATH6037 | Leave a comment

I am emailing a link of this to everyone on the class list every week. If you are not receiving these emails or want to have them sent to another email address feel free to email me at jpmccarthymaths@gmail.com and I will add you to the mailing list.

Continuous Assessment

Firstly an apology: question two on Quiz 2 was not in the Question Bank and I am sorry about this. Having said that, if you could do the other Integration by Parts questions, you should certainly have been able to do that one also. You really, really shouldn’t be learning off questions without understanding — it won’t serve you in the long run — the exam questions aren’t coming from a bank. Having said all that it was still unfair (and unintentional) so to make up for it we will have 11 quizzes rather than 10 (and still best out of eight). As far as I can see this is the fairest resolution.

Below find the results. You are identified by the last four digits of your student number unless you are winning the league. The individual quiz marks are out of 2.5 percentage points. Your best eight quizzes go to the 20% mark for quizzes. The R % column is your running percentage (for best eight quizzes), MPP is your Maple Percentage Points and the GPP is your Gross Percentage Points (for best eight quizzes and Maple).

The solutions to the last quiz may be found in the notes.

S/N Q1 Q2 Q3 Q4 Q5 Q6 Q7 Q8 Q9 Q10 Q11 R % QPP MPP GPP
Kelliher 2.5 2.5 100 5 1.5 6.5
3281 2.4 2.5 98 4.9 1.5 6.4
8335 2.4 2.5 97.5 4.875 1.5 6.375
5527 1.9 2.5 88 4.4 1.5 5.9
7878 2.2 2.2 87 4.35 1.5 5.85
1864 1.3 2.4 74 3.7 1.5 5.2
8478 1.9 1.72 72.4 3.62 1.5 5.12
2859 2.4 1 68 3.4 1.5 4.9
8416 2.3 1 66 3.3 1.5 4.8
8403 1.9 1.4 65 3.25 1.5 4.75
7209 1.9 1.2 62 3.1 1.5 4.6
2567 1.6 1.5 61 3.05 1.5 4.55
6548 1.6 1 51 2.55 1.5 4.05
NR 0.6 1.8 48 2.4 1.5 3.9
9464 1.2 0.9 42 2.1 1.5 3.6
8556 1.4 0.6 39 1.95 1.5 3.45
1852 0.7 1.2 38 1.9 1.5 3.4
5553 0.4 0.8 24 1.2 1.5 2.7
4198 0 1.2 24 1.2 1.5 2.7
8455 0.2 0.9 22 1.1 1.5 2.6
4775 0.5 0.3 16 0.8 1.5 2.3
5546 0 0 N/A 0 1.5 1.5

Read the rest of this entry »

MATH6037: Week 2

February 12, 2015 in MATH6037 | 6 comments

I am emailing a link of this to everyone on the class list every week. If you are not receiving these emails or want to have them sent to another email address feel free to email me at jpmccarthymaths@gmail.com and I will add you to the mailing list.

Note: We are supposed to be C212 rather than B212 as advertised by Conor.

Missing Manual

One of you left your manual somewhere… email me if you want it before Wednesday (I have it).

Quiz 1 Results and Solutions

Below find the results. You are identified by the last four digits of your student number unless you are winning the league. The marks are out of 2.5 percentage points. Your best eight quizzes go to the 20% mark for quizzes. The R % column is your running percentage (for best eight quizzes) and the GPP is your Gross Percentage Points (for best eight quizzes).

S/N Q1 Q2 Q3 Q4 Q5 Q6 Q7 Q8 Q9 Q10 R % GPP
Kelliher 2.5 100 2.5
3281 2.4 96 2.4
2859 2.4 96 2.4
8335 2.375 95 2.4
8416 2.3 92 2.3
7878 2.15 86 2.2
5527 1.9 76 1.9
7209 1.9 76 1.9
8478 1.9 76 1.9
8403 1.85 74 1.9
2567 1.55 62 1.6
6548 1.55 62 1.6
8556 1.35 54 1.4
1864 1.3 52 1.3
9464 1.2 48 1.2
1852 0.7 28 0.7
**** 0.6 24 0.6
**** 0.5 20 0.5
5553 0.4 16 0.4
8455 0.2 8 0.2
5546 0 0 0
4198 0 0 0

Read the rest of this entry »

MATH6037: Week 1

February 5, 2015 in MATH6037 | 14 comments

I am emailing a link of this to everyone on the class list every week. If you are not receiving these emails or want to have them sent to another email address feel free to email me at jpmccarthymaths@gmail.com and I will add you to the mailing list.

Note: We are supposed to be C212 rather than B212 as advertised by Conor.

Quiz 1 Question Bank

Please see here for your question bank for Quiz 1 (in Week 2). Here you can find the tables that will be allowed.

Quiz 1 runs from 19:00 to 19:15 sharp on Wednesday 11 February.

Continuous Assessment

The Continuous Assessment is broken into Weekly Quizzes (20%) and Maple (10%).

There will be ten weekly quizzes and your eight best results will count (so 2.5% per quiz from eight quizzes). You will receive an email (i.e. this one) on Thursday/Friday detailing the examinable exercises.

Maple consists of five labs and a Maple Test in the sixth lab. Satisfactory participation in labs gives you 1.5% and the Maple Test is worth 2.5%. More on this in the coming days.

Week 1

In Week 1 we explained the kind of thing that we would be looking at in this module. We did a quick review of integral calculus.

Week 2

In Week 2 we will look at u-substitutions. Then we will study Integration by Parts: this is the start of the new material (i.e. not MATH6019 material).

If we have a Maple lab we will do some basic plotting, differentiation and integration.

Week 6

As briefly mentioned in class, I will be away in Week 6 (11 March). I am proposing that we have a class over the Easter Break. In particular, I am thinking 1 April. Please email me if this not possible for you giving your reasons.

Notes

I have given out 15 sets of the notes. I received the €11 from everyone who got a manual. Please bring €11 for next week as more manuals will be printed. If you know someone who is not registered and who was absent in Week 1 please get them to email me at jpmccarthymaths@gmail.com so that I can order them a manual.

A student was asking did I have MATH6019-type notes that revision could be done with. You could look at an old higher level maths book, look in the library for anything with “Calculus” in the title.

Study

Please feel free to ask me questions about the exercises via email or even better on this webpage. Anyone can give me exercises they have done and I will correct them.

Student Resources

Please see the Student Resources tab on the top of this page for information on the Academic Learning Centre, etc..

MATH6037: Week 12

May 2, 2013 in MATH6037 | 6 comments

I am emailing a link of this to everyone on the class list every week. If you are not receiving these emails or want to have them sent to another email address feel free to email me at jpmccarthymaths@gmail.com and I will add you to the mailing list.

Continuous Assessment Results

You are identified by the last four digits of your student number. The first column is your Test 1 result while the second is your Maple Labs participation. The third is your Maple Test Mark out of 5. The fourth is your continuous assessment mark out of 30. The last is the percentage you must have on the final to pass. If you have any issues with this please email me.

Student Number Test Maple Labs Maple Test CA Mark Pass
8272 93 10 5 28.95 15.79
4673 90 10 3 26.5 19.29
1054 78 10 4 25.7 20.43
9455 65 10 5 24.75 21.79
0902 70 10 3 23.5 23.57
2344 61 10 3 22.15 25.50
2352 58 10 2 20.7 27.57
4346 28 10 3 17.2 32.57
3152 40 10 1 17 32.86
2343 25 10 3 16.75 33.21
2351 15 8 3 13.25 38.21
2345 28 6 3 13.2 38.29
4674 48 4 0 11.2 41.14
3150 25 6 0 9.75 43.21
1215 0 6 2 8 45.71
8171 30 0 0 4.5 50.71

Study

Please feel free to ask me questions via email or even better on this webpage — especially those of us who struggled in the test.

Please find a reference for some of the prerequisite material here.

Week 12

We finished our work on Laplace Methods and looked at the general solution of the damped harmonic oscillator. The following is the correct way to categorise over and underdamping:

Damped Harmonic Oscillator Analysis

The differential equation

\displaystyle m\frac{d^2x}{dt^2}+\lambda \frac{dx}{dt}+kx(t)=0,

as discussed on page 154 is the equation of a damped harmonic oscillator. There are three behaviours. One way to analyse these is to define the following parameters

\displaystyle \gamma=\frac{\lambda}{2m}, \displaystyle \omega_0=\sqrt{\frac{k}{m}}

and follow the analysis as per the notes. However last night 8 May we outlined an even easier analysis.

First write the differential equation as it will be on your exam paper

\displaystyle \frac{d^2x}{dt^2}+b\cdot \frac{dx}{dt}+c\cdot x(t)=0.

Now find the Laplace Transform of the solution. It will look like

\displaystyle X(s)=\frac{As+B}{s^2+bs+c}.

Now there are three cases depending on whether s^2+bs+c has two distinct real roots, equal real roots, or complex roots. Note in all cases a=1.

Underdamping b^2-4ac<0

In this case the roots are complex: no real roots implying no real factors hence we must complete the square

\displaystyle X(s)=\frac{As+B}{(s+a)^2+k^2}

which is composed of shifted sines and cosines when we transform it back

\displaystyle x(t)=Ce^{-at}\cos kt+De^{-at}\sin kt

Overdamping b^2-4ac>0

In this case the roots are real and distinct so we have two factors and hence a partial fraction expansion like this:

\displaystyle X(s)=\frac{As+B}{s^2+bs+c}=\frac{As+B}{(s+\alpha)(s+\beta)}=\frac{C}{s+\alpha}+\frac{D}{s+\beta},

which is composed of two exponentially decaying terms when we transform back.

\displaystyle x(t)=Ce^{-\alpha t}+De^{-\beta t}

Critical Damping 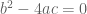b^2-4ac=0

In this case the root are real and repeated hence we have repeated real factors and hence a partial fraction expansion like this:

\displaystyle X(s)=\frac{As+B}{s^2+bs+c}=\frac{As+B}{(s+\alpha)^2}=\frac{C}{s+\alpha}+\frac{D}{(s+\alpha)^2},

which is composed of an exponentially decaying term and (before transforming) a shifted \displaystyle \frac{1}{s^2} which will need the First Shift Theorem when we transform back:

\displaystyle x(t)=Ce^{-\alpha t}+Dte^{-\alpha t}

In Conclusion

If you are asked to analyse a damped harmonic oscillator of the form

m\frac{d^2x}{dt^2}+\lambda \frac{dx}{dt}+kx(t)=0,

then you have three options:

  1. Calculate b^2-4ac. Over-zero = Over-damping, Under-zero = Under-damping and Equal Zero = Critical-damping
  2. Calculate \gamma and \omega_0 as described on page 154 of the notes and compare. It is actually equivalent to method 1. In the Laplace marking scheme handout a damped harmonic oscillator is analysed using this method.
  3. Solve the differential equation using Laplace Methods and see which behaviour the solution corresponds to.

Week 13

We will hold a review tutorial on Wednesday 8 May in the usual room. First off, the layout of your exam is the same as Winter 2012: do question one worth 50/100 and two out of questions two, three, four; each worth 25/100.

I will field any questions ye might have at this time and if there are no questions we will do the exam paper from Autumn 2012.

Formulae to Learn?

Somebody asked me for a list of formulae that ye might need that are not on the tables. I would put the following on that list:

  • The Midpoint Rule Formula Here

One could include

  • The Differential; if z=f(x,y) then \displaystyle\Delta z\approx dz=\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y

There are a number of others such as \displaystyle \int_a^\infty=\lim_{R\rightarrow\infty}\int_a^R for example but these are ideas rather than formulae really. Can you think of any others (the Euler method formula will be given to you)?

Math.Stack Exchange

If you find yourself stuck and for some reason feel unable to ask me the question you could do worse than go to the excellent site math.stackexchange.com. If you are nice and polite, and show due deference to these principles you will find that your questions are answered promptly. For example this question about completing the square.

MATH6037: Week 11

April 29, 2013 in MATH6037 | 2 comments

I am emailing a link of this to everyone on the class list every week. If you are not receiving these emails or want to have them sent to another email address feel free to email me at jpmccarthymaths@gmail.com and I will add you to the mailing list.

Maple Test

I have given ye a sample Maple Test and ye will have your Maple Test Wednesday at 20:30.

Study

Please feel free to ask me questions via email or even better on this webpage — especially those of us who struggled in the test.

Please find a reference for some of the prerequisite material here.

Week 11

We continued our study of Laplace Methods and saw how they can solve differential equations.

Weeks 12

We finish our work on Laplace Methods and look at the general solution of the damped harmonic oscillator.

Week 13

We will hold a review tutorial on Wednesday 8 May in the usual room. First off, the layout of your exam is the same as Winter 2012: do question one worth 50/100 and two out of questions two, three, four; each worth 25/100.

I will field any questions ye might have at this time and if there are no questions we will do the exam paper from Autumn 2012.

Math.Stack Exchange

If you find yourself stuck and for some reason feel unable to ask me the question you could do worse than go to the excellent site math.stackexchange.com. If you are nice and polite, and show due deference to these principles you will find that your questions are answered promptly. For example this question about generalising what we will be doing in the next question.

MATH6037: Week 10

April 19, 2013 in MATH6037 | 2 comments

I am emailing a link of this to everyone on the class list every week. If you are not receiving these emails or want to have them sent to another email address feel free to email me at jpmccarthymaths@gmail.com and I will add you to the mailing list.

Maple Test

I have given ye a sample Maple Testt and ye will have your Maple Test in Week 12.

Study

Please feel free to ask me questions via email or even better on this webpage — especially those of us who struggled in the test.

Please find a reference for some of the prerequisite material here.

Week 10

We continued our study of Laplace Methods with a review of partial fractions. We also spoke about the inverse of the Laplace transform. I also gave out solutions of the Winter 2012 Laplace questions so that ye can see how I mark these questions.

Weeks 11 & 12

We continue our work on Laplace Methods and see how they can solve differential equations.

Week 13

We will do the exam paper from Summer 2012.

Math.Stack Exchange

If you find yourself stuck and for some reason feel unable to ask me the question you could do worse than go to the excellent site math.stackexchange.com. If you are nice and polite, and show due deference to these principles you will find that your questions are answered promptly. For example this rather technical question about the inverse Laplace transform.